filmov
tv
Introduction to Volumes by Cylindrical Shells: Visual Comparison with Slicing

Показать описание
I tried to put on my magician's hat as best as I could for this one. :)
Calculating Volume by Cylindrical Shells
How to Find the Volume of a Cylinder | Math with Mr. J
Math Antics - Volume
Introduction to Volumes by Cylindrical Shells: Visual Comparison with Slicing
Volume of a Cylinder and Surface Area of a Cylinder
Volume of a Cylinder
Calculus 1 Lecture 5.3: Volume of Solids By Cylindrical Shells Method
Introduction to volumes of revolution by cylindrical shells
ex 12.1 Q 4,5 CLASS 10TH CHAPTER 12 SURFACE AREAS AND VOLUMES|| #10THMATHS #EDUCATIONCHANNEL
Volumes: The Cylindrical Shell Method.
How to Calculate the Volume of a Cylinder
Volumes by Shells (2 of 3: Introduction to Cylindrical Shells & finding typical volume)
Disk/Washer vs. Cylindrical Shell...when to use which?
Volume by Cylindrical Shells (3 of 3: Finding the Volume via Cylindrical Shells and which to choose)
Volume of Revolution (Cylindrical Shells)
Volumes by Cylindrical Shells (example question from exam)
Volumes by Cylindrical Shells
6.3.1 Volumes by Cylindrical Shells - Introduction
VOLUME with CYLINDRICAL SHELLS - CALCULUS
Integrals and Volumes by Cylindrical Shells
Calculating the Volume of a Solid of Revolution by Integration
Applications of Integration: Volume by cylindrical shell - 01. Introduction
The Concept of Cylindrical Shells to find Volume
Volume (Integration) Using Cylindrical Shells Method
Комментарии
 0:07:40
0:07:40
 0:03:57
0:03:57
 0:12:36
0:12:36
 0:10:20
0:10:20
 0:11:14
0:11:14
 0:01:43
0:01:43
 0:54:56
0:54:56
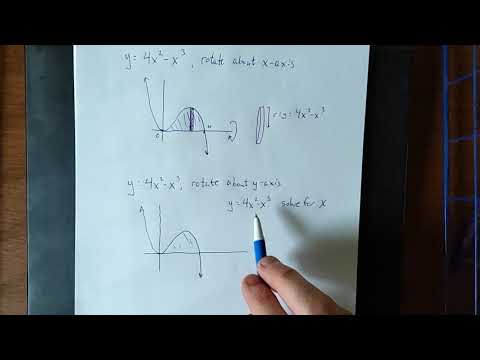 0:03:27
0:03:27
 0:12:26
0:12:26
 0:43:54
0:43:54
 0:00:31
0:00:31
 0:09:31
0:09:31
 0:13:11
0:13:11
 0:07:20
0:07:20
 0:04:02
0:04:02
 0:06:49
0:06:49
 0:46:18
0:46:18
 0:10:55
0:10:55
 0:14:55
0:14:55
 0:13:17
0:13:17
 0:11:20
0:11:20
 0:06:36
0:06:36
 0:12:14
0:12:14
 0:13:53
0:13:53