filmov
tv
Conditional Probability (4 of 4: Determining reduced sample space)

Показать описание
Conditional Probability (4 of 4: Determining reduced sample space)
Conditional Probability 4 | Application of Bayes' Theorem
Conditional Probability (4 of 9: Using Two-Way Tables)
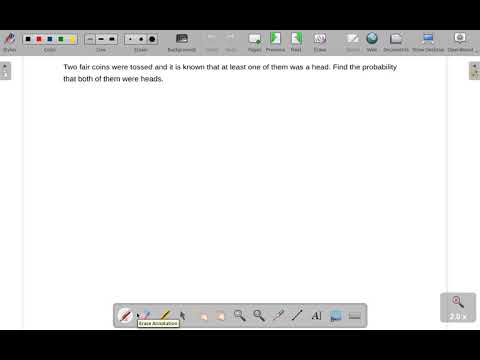
Intro to Conditional Probability
Conditional Probability | GCSE Maths 2025
AP Stats Unit 4 Ch 5 Probability #4: Conditional Probability
Conditional Probability Example
Conditional probability -- Example 4
Statistics and probability basics
Conditional Probability (3 of 4: Defective light bulbs)
Year 10 5.3 Probability 4 - Formal Notation for conditional probability
Conditional Probability (4 of 7: Using formal condition notation)
Conditional probability in one minute
Conditional Probability and Risk (4/4) | Probability - NCEA Level 2 Maths | StudyTime NZ
Conditional Probabilities: What is the probability that 4 horses place 1 through 4?
4 - Conditional Probability
M115 7.5-5 Conditional Probability Example 4
Differences in Conditional Probabilities: S-CP.4
VCE Maths Methods - Introduction to Probability - 4 - conditional probability
Probability and Statistics Lesson 72: Continuous Uniform Distribution, Conditional Probability
Class 12th – Conditional Probability Result-4 | Probability | Tutorials Point
Conditional Probability | Lecture 4 | Probability Course
11-4 Conditional Probability
4-2 Conditional Probability
Комментарии
 0:08:51
0:08:51
 0:14:06
0:14:06
 0:07:49
0:07:49
 0:06:14
0:06:14
 0:00:57
0:00:57
 0:20:26
0:20:26
 0:04:21
0:04:21
 0:06:19
0:06:19
 11:01:01
11:01:01
 0:07:16
0:07:16
 0:11:52
0:11:52
 0:08:06
0:08:06
 0:00:54
0:00:54
 0:06:57
0:06:57
 0:02:48
0:02:48
 0:09:47
0:09:47
 0:03:06
0:03:06
 0:02:34
0:02:34
 0:06:38
0:06:38
 0:05:18
0:05:18
 0:00:54
0:00:54
 0:06:05
0:06:05
 0:07:33
0:07:33
 0:04:26
0:04:26