filmov
tv
Upper Bound for Integral of e^(iz)/z over a semicircle

Показать описание
Today, we show that the integral of e^(iz)/z over a semicircular arc goes to 0 as the radius goes to infinity.
Original video (sin(x)/x using complex analysis):
Original video (sin(x)/x using complex analysis):
Upper bound for integral
Upper Bound for Integral of e^(iz)/z over a semicircle
142. Upper bounds for moduli of complex Integrals
143. example 1 Upper bounds for moduli of complex Integrals
Upper and Lower Integrals
Complex Integration: The ML Inequality Proof and Example
Integral with upper and lower bound being the same
Example of a Double Integral using Polar Coordinates
Contour Integral part 3| Upper Bound for Moduli of Contur Integral | ML- Inequality Complex Analysis
EXAMPLE: Using upper and lower sums to bound a definite integral
Learn to evaluate the integral with functions as bounds
Use Properties of Integrals To Show That an Integral is Bounded
Definite integrals with an unknown bound
Lemma Upper bound of gaussian arctan integral
Upper bounds for moduli of complex integral
Complex integration important theorem 🔥
Switching bounds of definite integral | AP Calculus AB | Khan Academy
Upper Bound
Real Analysis 6 | Supremum and Infimum
Learn how to find the derivative of the integral
PotW: Upper Bound of a Sum [Algebra]
How to Set Up Double Integrals
First result about the integral of two functions. The upper bound for the product of two functions.
Fundamental Theorem of Calculus Part 1
Комментарии
 0:01:32
0:01:32
 0:15:34
0:15:34
 0:07:12
0:07:12
 0:10:34
0:10:34
 0:17:51
0:17:51
 0:10:51
0:10:51
 0:00:31
0:00:31
 0:06:57
0:06:57
 0:21:04
0:21:04
 0:03:22
0:03:22
 0:02:04
0:02:04
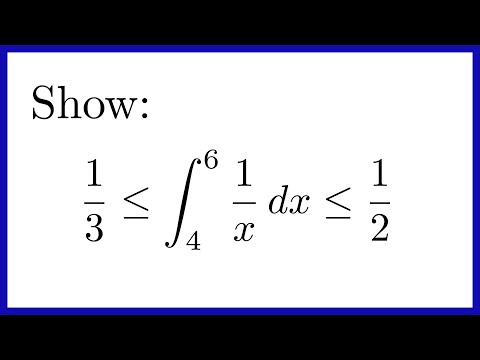 0:02:10
0:02:10
 0:02:25
0:02:25
 0:01:39
0:01:39
 0:01:01
0:01:01
 0:04:42
0:04:42
 0:04:37
0:04:37
 0:10:26
0:10:26
 0:09:10
0:09:10
 0:01:25
0:01:25
 0:02:25
0:02:25
 0:08:56
0:08:56
 0:08:37
0:08:37
 0:11:30
0:11:30