filmov
tv
Solve a Cubic Polynomial Inequality Using Boundary Points

Показать описание
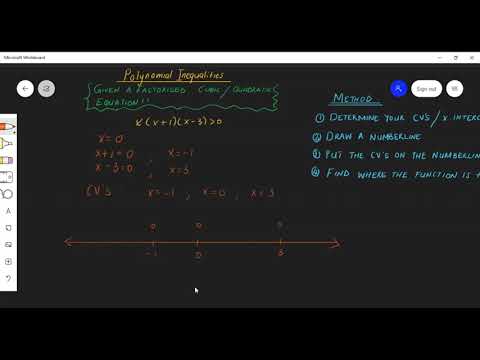
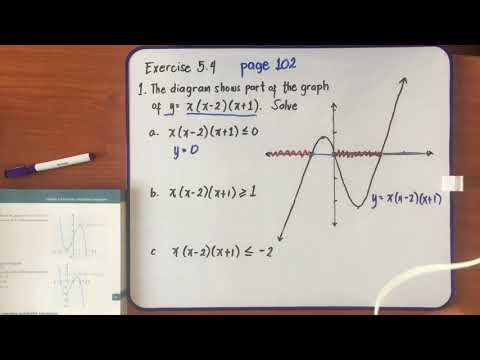
x^3+3x^2-9x-27 is greater than or equal to 0 is the polynomial inequality to be solved. The four steps in solving a polynomial inequality using boundary points (critical points) are explained. (1) The inequality symbol is replaced by an equal sign and this polynomial equation is solved using factoring by grouping. The solutions to this equation are the boundary points and these are the only points at which the inequality can change from true to false or from false to true. (2) The boundary points are plotted on the number line and they separate the number line into three regions. (3) One test value in each region is used to see if the inequality is true or false and the solution to the inequality contains all the regions where the inequality is true. (4) Finally the decision is made on whether to include or exclude the boundary points from the solution set.
Timestamps:
0:00 Introduction
0:31 Steps for Solving Polynomial Inequalities
1:00 Finding Boundary Points
4:17 Intervals on Number Line
5:13 Test Values in Each Region
8:13 Interval Notation
Timestamps:
0:00 Introduction
0:31 Steps for Solving Polynomial Inequalities
1:00 Finding Boundary Points
4:17 Intervals on Number Line
5:13 Test Values in Each Region
8:13 Interval Notation
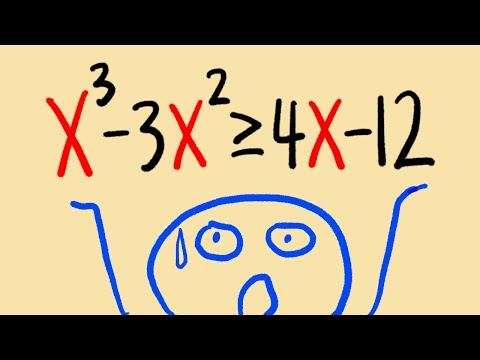 0:03:33
0:03:33
 0:12:56
0:12:56
 0:09:58
0:09:58
 0:07:04
0:07:04
 0:03:29
0:03:29
 0:06:05
0:06:05
 0:17:11
0:17:11
 0:07:58
0:07:58
 0:10:52
0:10:52
 0:05:14
0:05:14
 0:00:50
0:00:50
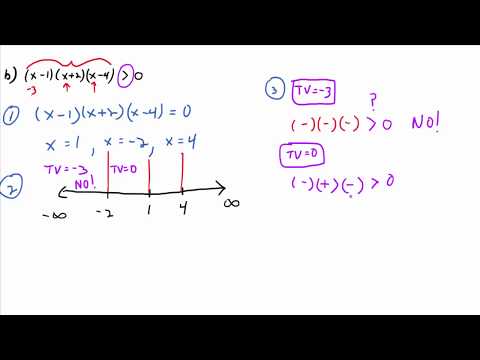 0:06:57
0:06:57
 0:00:37
0:00:37
 0:02:18
0:02:18
 0:10:28
0:10:28
 0:08:14
0:08:14
 0:34:05
0:34:05
 0:09:08
0:09:08
 0:00:34
0:00:34
 0:19:10
0:19:10
 0:07:18
0:07:18
 0:08:01
0:08:01
 0:13:18
0:13:18
 0:04:27
0:04:27