filmov
tv
Linear Algebra 34 | Range and Kernel of a Matrix

Показать описание
Thanks to all supporters! They are mentioned in the credits of the video :)
This is my video series about Linear Algebra. I hope that it will help everyone who wants to learn about it.
#LinearAlgebra
#Vectors
#Matrices
#MachineLearning
#Eigenvalues
#Calculus
#Mathematics
(This explanation fits to lectures for students in their first year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
Linear Algebra 34 | Range and Kernel of a Matrix
Linear Algebra 34 | Range and Kernel of a Matrix [dark version]
Linear Algebra 34, Vectors Distance, examples
34. Distance Matrices, Procrustes Problem
How to Find the Rank of a Matrix (with echelon form) | Linear Algebra
Given a linear transformation, find the kernel and range
NEWYES Calculator VS Casio calculator
Null space and column space basis | Vectors and spaces | Linear Algebra | Khan Academy
Normed vector space: definition and examples of vector and matrix norms
Range of a Linear Transformation
How to Find the Matrix of a Linear Transformation
The rank of a matrix
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Kernel and Image of a Linear Transformation Example 1 | Linear Algebra | Griti
Linear Algebra - Lecture 27: The Range and Null Space of a Matrix
Identify the Domain and Codomain of a Linear Transformation Given a Matrix
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Range Space of Linear Transformation
Trying transition video for the first time 💙😂 || #transformation #transition #shorts #viralvideo...
Determine a Basis for the Kernel of a Matrix Transformation (3 by 4)
The Hardest Math Test
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Range of a Matrix aka Column Space
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
Комментарии
 0:08:58
0:08:58
 0:08:58
0:08:58
 0:06:12
0:06:12
 0:29:17
0:29:17
 0:03:25
0:03:25
 0:08:25
0:08:25
 0:00:14
0:00:14
 0:25:13
0:25:13
 0:45:02
0:45:02
 0:06:09
0:06:09
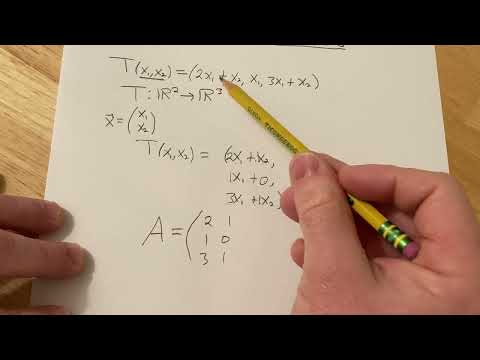 0:05:19
0:05:19
 0:17:17
0:17:17
 0:10:59
0:10:59
 0:06:06
0:06:06
 0:13:49
0:13:49
 0:02:45
0:02:45
 0:00:16
0:00:16
 0:08:44
0:08:44
 0:00:15
0:00:15
 0:04:16
0:04:16
 0:00:28
0:00:28
 0:00:15
0:00:15
 0:10:41
0:10:41
 0:13:52
0:13:52