filmov
tv
Perpendicular Bisector of a Line Segment and Triangle

Показать описание
This geometry video tutorial provides a basic introduction into the perpendicular bisector of a line segment and a triangle. it discusses the perpendicular bisector theorem and the definition of perpendicular bisectors in addition to how to use them in a geometry two column proof problem with statements and reasons. This tutorial also describes how to identify the location of the circumcenter of a acute, right, and obtuse triangle after drawing all 3 altitudes from the vertex of the triangle to the midpoint of the opposite. This video contains plenty of examples and geometry practice problems.
Triangle Congruence - SSS, SAS, ASA:
CPCTC - 2 Column Proofs With Triangles:
Hypotenuse Leg Theorem - HL Postulate:
Detour Proofs - Double Triangle Congruence:
___________________________________
The Midpoint Formula:
Missing Diagrams - 2 Column Proofs:
Right Angle Theorem - SSS & SAS:
Altitude, Median, Midpoint & P. Bisector:
Parallel & Perpendicular Lines - Slope:
__________________________________
Indirect Proofs - Example Problems:
Proving Parallel Lines With Proofs:
The Exterior Angle Theorem:
Exterior Angle Inequality Theorem:
Polygons:
_______________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Triangle Congruence - SSS, SAS, ASA:
CPCTC - 2 Column Proofs With Triangles:
Hypotenuse Leg Theorem - HL Postulate:
Detour Proofs - Double Triangle Congruence:
___________________________________
The Midpoint Formula:
Missing Diagrams - 2 Column Proofs:
Right Angle Theorem - SSS & SAS:
Altitude, Median, Midpoint & P. Bisector:
Parallel & Perpendicular Lines - Slope:
__________________________________
Indirect Proofs - Example Problems:
Proving Parallel Lines With Proofs:
The Exterior Angle Theorem:
Exterior Angle Inequality Theorem:
Polygons:
_______________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Комментарии
 0:01:11
0:01:11
 0:01:22
0:01:22
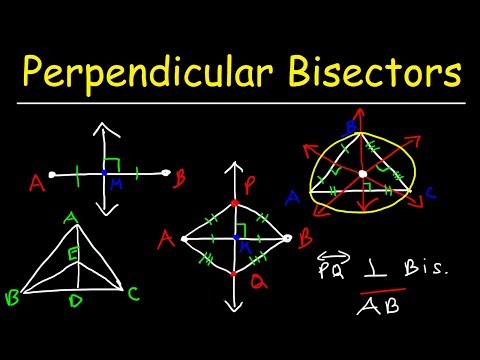 0:21:44
0:21:44
 0:01:11
0:01:11
 0:06:13
0:06:13
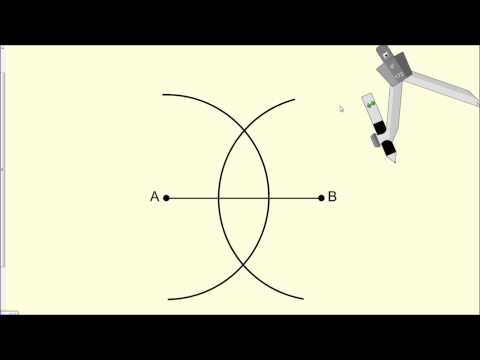 0:03:11
0:03:11
 0:02:51
0:02:51
 0:07:23
0:07:23
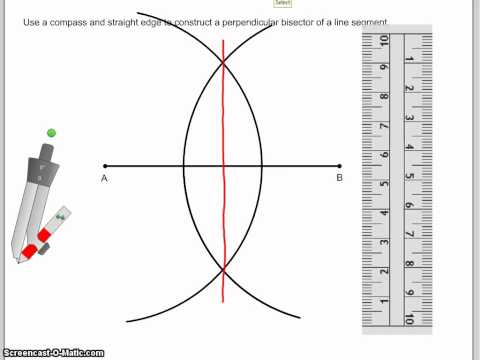 0:03:15
0:03:15
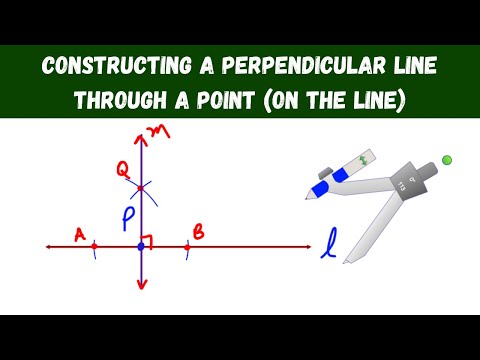 0:01:28
0:01:28
 0:01:42
0:01:42
 0:08:29
0:08:29
 0:00:52
0:00:52
 0:02:24
0:02:24
 0:04:26
0:04:26
 0:03:20
0:03:20
 0:07:38
0:07:38
 0:02:22
0:02:22
 0:04:45
0:04:45
 0:04:14
0:04:14
 0:01:39
0:01:39
 0:04:51
0:04:51
 0:01:11
0:01:11
 0:01:23
0:01:23