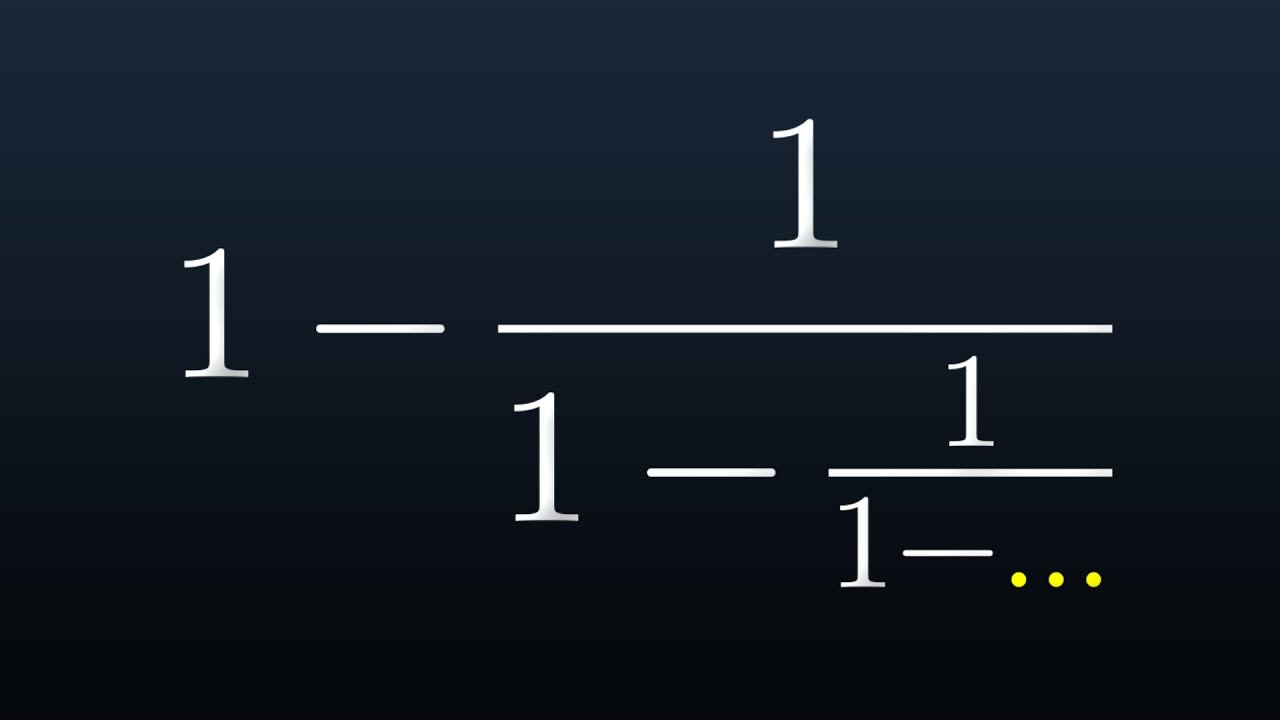
Why Isn't This Fraction Real?

🙏Support me by becoming a channel member!

Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.

#math #brithemathguy #goldenratio

[BriTheMathGuy]

🎓Become a Math Master With My Intro To Proofs Course! (FREE ON YOUTUBE)

[angelmendez-rivera]

You deal with this rigorously by defining looking at sequences on R defined by the recursion s(n + 1) = 1 – 1/s(n), and looking at how the convergence properties change as a function of s(0). If s converges for all s(0), and the limit is the same for all s(0), then the continued fraction is well-defined, and is defined to be equal to that limit. To analyze this, notice that s(n + 1) = f(s(n)), where f : R\{0} —> R\{1} such that f(t) = 1 – 1/t. This makes this a fixed-point iteration. Because f is singular at 0, there certain values of s(0) that will make the iteration crash. To find those, we must first realize that f(f(t)) = 1 – 1/(1 – 1/t) = 1 – t/(t – 1) = 1/(1 – t) = f^(–1)(t), meaning that f(f(f(t))) = t everywhere, so long as t is not equal to 0 or 1. As such, we can redefine f so that f : R\{0, 1} —> R\{0, 1}, f(t) = 1 – 1/t everywhere. This ensures that f^m is well-defined for every m, and has the same singularities as f.

Now, here, with the discovery that (f^3)(t) = t everywhere, you realize that s(1) = 1 – 1/s(0), s(2) = 1/(1 – s(0)), and that s(m + 3) = s(m) for all m. This means s is a periodic, oscillating sequence. Therefore, it converges if and only if s(0) = s(1) = s(2). However, this is impossible in the real numbers, but it is possible in the complex numbers. Using the complex numbers is fine, since as a topological field, it is an extremely natural extension of the real numbers. This is to say that the way convergence works for complex numbers is just the same as the convergence for real numbers. So, it is perfectly fine to say that if s(0) = 1 – 1/s(0) = 1/(1 – s(0)), then s converges. If s converges, it necessarily converges to s(0), since s would be a constant sequence. Although, to get technical about it, if you are working in an arbitrary topological ring, then what values are possible depends on the ring as well as the topology. In the complex numbers, s(0) = 1 – 1/s(0) implies s(0)^2 = s(0) – 1, meaning s(0)^2 – s(0) + 1 = 0, while s(0) = 1/(1 – s(0)) implies s(0) – s(0)^2 = 1, which translates to the same equation, s(0)^2 – s(0) + 1 = 0. That leaves us with two possible values of s(0), with two limits, one for each. However, since the limit depends on s(0), and is in fact equal to s(0), the continued fraction is ill-defined.

[Matthew_Klepadlo]

0 and 1 may appear just like simple numbers at first, but there’s so much interesting, fascinating complexity and universality ingrained in their very essence…

These classic numbers are so cool!

[Inspirator_AG]

The reason 'it is not real' is because infinity tends to be irregular (And an assumption has been made.).

[wiggles]

The problem is to define the first term in the sequence. For some choices, an nth term is undefined. For other choices, the 4th term in the sequence equals the 1st term. There are no other outcomes. This sequence is a great example of a sequence where you can calculate a limit but the limit doesn't actually exist.

[eliaperli]

Also, maybe someone doesn't know this:
For every succession of real numbers, if such succession has a limit, that limit must be a real number (because R is a closed set)

[MichaelRothwell]

Nice! At first I thought you were trying to pull our leg - to really convince us that the continued fraction converges to one of the two non-real cube roots of -1 (no idea why it would be one and not the other, BTW). So it was quite a relief when you brought up the "subtle" issue of convergence, not to mention actually having a look at the values of the first few terms...

The point is a well made, since you frequently see problems where you are to find the value of some infinitely nested expression (power tower, nested surds, continued fractions, for example). And very often the resolution is very naive, working out the limit straight away, when the first steps should be translating the problem into a recursively defined sequence, then establishing (or otherwise) convergence (often with useful constraints on the limit in the process). Only then (assuming convergence was established) is one entitled to calculate the limit.

Just one small point: to be complete, the definition of a recursively defined sequence requires not only the recursive relation, but also the value of the first term.

[threepointone]

Speaking of continued fractions, here are some formulas:

1. n+n/(n+n/(n+…))
Let x=n+n/(n+n/(n+…))
x=n+n/x
*multiply both sides by x*
x^2=nx+n
x^2-nx-n=0
*use quadratic formula*
x=(n±√(n^2+4n))/2

2. n+1/(n+1/(n+…))
Let x=n+1/(n+1/(n+…))
x=n+1/x
*multiply by x*
x^2=nx+1
x^2-nx-1=0
*use quadratic formula*
x=(n±√(n^2+4))/2

3. n-n/(n-n/(n-…))
Let x=n-n/(n-n/(n-…))
x=n-n/x
*multiply by x*
x^2=nx-n
x^2-nx+n=0
*use quadratic formula*
x=(n ± √(n^2-4n))/2

4. n-1/(n-1/(n-…))
Let x=n-1/(n-1/(n-…))
x=n-1/x
*multiply by x*
x^2=nx-1
x^2-nx+1=0
*use quadratic formula*
x=(n±√(n^2-4))/2

[glowstonelovepad]

Is the continued fraction 5-(6/(5-(6/(5-(6/... 2 or 3?

[brahmbandyopadhyay]

1:33 1.6 number, aka the Golden Ratio. Lol

[taleladar]

I'm not so sure about this, Bri. As you point out, the fraction in question is composed of nothing but real numbers. So how DOES it end up having a complex solution?

... well like in most other math problems, you can ALMOST ALWAYS discover complex solutions if you decide to delve into the complex numbers and find them. The issue here is that when you set up the fraction to behave recursively, you are assuming that EVERY STEP of the next recursion is exactly the same as the last. In this sense, with these stricter criteria, there is no real solution and only a complex solution.

However, if we were to start from the bottom and use pi as the x, the positive version always ends up converging to the golden ratio no matter what number you use. However the negative version flips around between 3 different values.

When using pi as the guinea pig, these numbers are 0.682, -0.467, and 3.142. Or pi.

If I were to use the square root of 2, I'd get 0.293, -2.414, and 1.414, and it also keeps repeating these values.

I think every real number you try plugging in will bounce around between three different values, except for 0 and 1 which will cause the fraction to divide by zero and be invalid. So if I were to be fast and loose, I'd say that fraction could potentially be equal to any real number - except for 0 or 1. But then again, since it does not converge and would always be bouncing around between three different values, I wouldn't know what that is called.

[bringonthevelocirapture]

If you replace all the ones with the variable x, and use each division/addition combo as an iteration with the final term being x/(x+1), you can integrate each iteration, and the resulting equation has a direct relationship with the Fibonacci numbers directly with the iteration, n.

So, if n=4, f(x)=x/(x+x/(x+x/(x+1))) (from Fibonacci when n(1)=0: 0, 1, 1, 2, 3),

the integral is (I have actually checked these manually and online) : [ln(2x+3)+2]/4

and you define "c" as the nth term in the Fibonacci sequence and "d" as the following number in the sequence, every single integral of every nth iteration can be written out as:



I think that's pretty cool. I call them the Fibonacci integrals. Because I can.

[Pabloable]

I ought to have realized where this was going, since I’ve toyed around with f(x)=1-1/x in the past. Fun fact: f(f(f(x)))=x, at least where x≠0 and x≠1, or if you extend it to include the point at infinity and say that based on asymptotics f(∞)=1.

[ethangibson]

Could we not simply represent this fraction as infinite nested geometric series?

[Bolpat]

I have nothing against sponsored content, but this one took like half of the video and your black background is nice, but the sponsor part is bright as sunlight.

[kickstorm]

When Bri posts a video about a nuber you saw in maths class 3 days prior, you know it was meant to be this way all along.

[MrRenanwill]

The set of the real numbers are closed in the set of the complex numbers. This means that every sequence of real numbers converges to real numbers, If they converge.

[georgebayliss]

I wanted to mention that you may want to be careful with how you promote Wren.

I absolutely agree with helping our planet but consumer carbon offset projects are a little problematic. They propagate the idea that the climate crisis is all our collective fault when certain industries and leaders are disproportionately at fault and have yet to reform themselves.

Also certain “rainforest protection” projects actually displace indigenous population with sustainable carbon lifestyles in the name of protecting the land.

I acknowledge that I bring some bias into this comment due to the specific literature I’ve read but I thought I should bring up these points.

[lukandrate]

It doesn't converge to a complex number. It diverges. If you type this thing into a calculator it oscillates between undefined(1/0→±∞) and undefined(1/(1-1/0)→0) and also R is a closed set

[KingGrio]

So does the continued fraction in the thumbnail have anything to do with the complex number or not ?