Elchanan Solomon (10/16/18): An intrinsic persistent homology transform

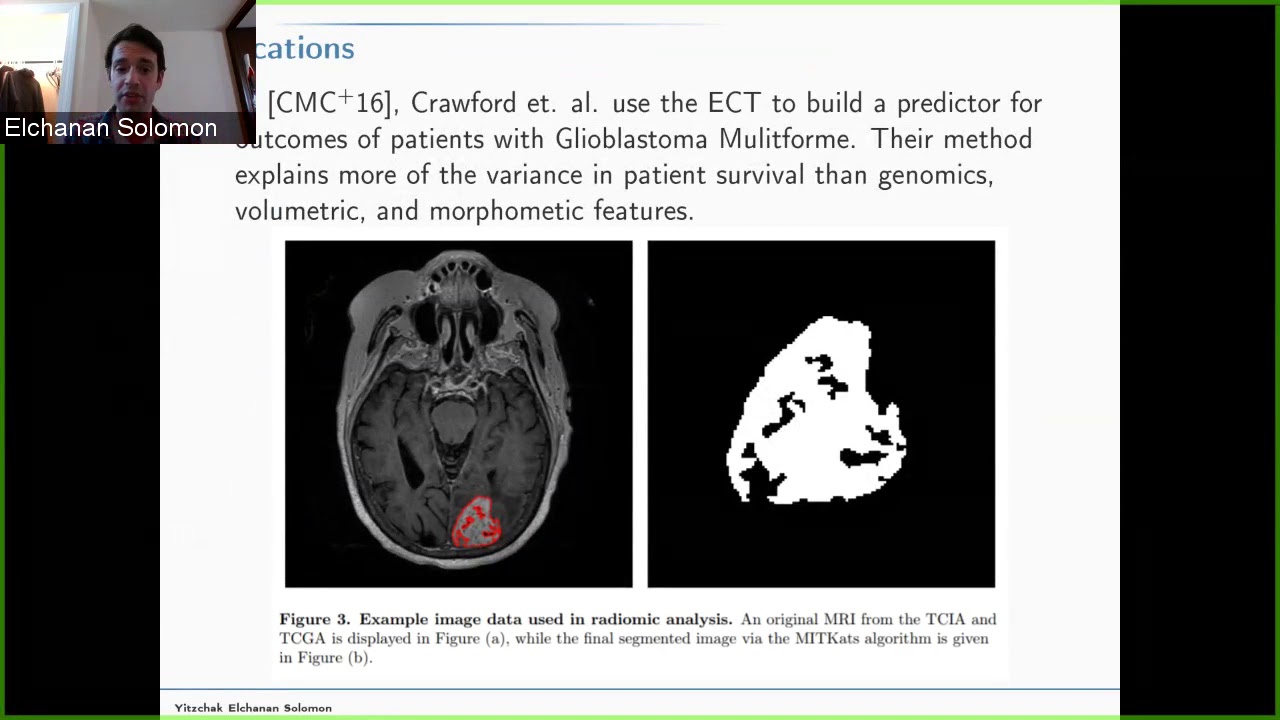
The Persistent Homology Transform (PHT) and Euler Characteristic Transform (ECT), first proposed by Turner, Mukherjee, and Boyer, were the first TDA invariants shown to be injective on the space of shapes embedded in Euclidean space. A number of recent papers have presented new, elegant new proofs of this fact, demonstrated finiteness results, and explored applications. In this talk, I will discuss joint work with Steve Oudot that studies an analogue of this construction for intrinsic metric spaces, focusing on the case of metric graphs. Although this Intrinsic Persistent Homology Transform (IPHT) is no longer injective (originally observed by Dey, Shi, and Wang), we show that it enjoys a number of injectivity results: in particular, it is generically injective in the appropriate topology.