filmov
tv
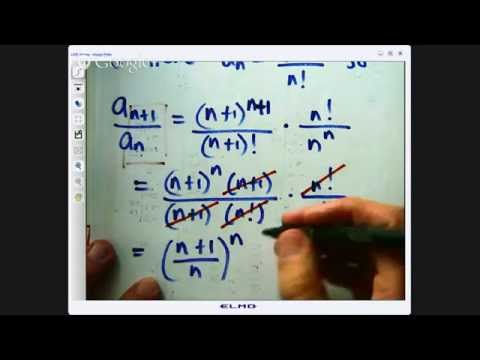
The Ratio Test - Proof of Part (a)

Показать описание
The Ratio Test - Proof of Part (a)
Ratio Test Proof
The Ratio Test - Proof of Part (b)
The Ratio Test - Proof of Part (c)
Statement and Proof of The Ratio Test (convergence)
Proof of the Ratio Test
Ratio and Root Test - Video 3 - Proof of the Ratio Test
Proof of the Ratio Test
12 divided by 6 over 3×4. Many could not do it right! Ukraine Math Test #math #percentages #ukraine...
11.6 Proof of Ratio Test
Ratio & Root Tests | Geometric Series Generalized
Ratio Test
Proof of ratio test
Proof of the Ratio Test
The Ratio Test - Introduction
Ratio Test to test for convergence! #mathematics #calculushelp #calculus #series #mathtricks
Proof of the Ratio Test for Infinite Series
Pre-Ratio Test
The Ratio Test
Ratio test for series and simple proof!
Ratio test proof 1
How To Use The Ratio Test
13.18 Ratio test: the theorem
Ratio Test for Sequences
Комментарии
 0:10:26
0:10:26
 0:10:42
0:10:42
 0:13:38
0:13:38
 0:07:22
0:07:22
 0:06:36
0:06:36
 0:09:12
0:09:12
 0:06:08
0:06:08
 0:21:21
0:21:21
 0:00:55
0:00:55
 0:13:53
0:13:53
 0:09:12
0:09:12
 0:27:56
0:27:56
 0:20:54
0:20:54
 0:23:14
0:23:14
 0:05:06
0:05:06
 0:00:21
0:00:21
 0:06:56
0:06:56
 0:17:39
0:17:39
 1:06:29
1:06:29
 0:19:11
0:19:11
 0:16:22
0:16:22
 0:05:43
0:05:43
 0:05:17
0:05:17
 0:04:33
0:04:33