filmov
tv
Computing the System Frequency Response from Difference Equation

Показать описание
In the previous video, we introduced the Frequency Response H(omega) as an important system quantity that describes how the amplitude and phase of each frequency component of a signal are changed. As we continue to review related concepts, this video examines how to compute the Frequency Response H(Omega) of a discrete-time system when given the time-domain difference equation of the system. Our strategy in this case is to take the Z-transform of the difference equation to find the system transfer function H(z). Then, we evaluate the transfer function on the unit circle by letting z = exp(j*Omega). This yields the desired frequency response H(Omega).
The next video in this playlist is:
The previous video in this playlist is:
Join the channel for membership perks:
Course website:
A quick introduction to frequency response
Intro to Control - 14.1 Frequency Response
TV8V8-Impulse Response from Frequency Response
Frequency Response Descriptions for LTI Systems
Introduction to Frequency Response
Electrical Engineering: Ch 15: Frequency Response (18 of 56) Bode Plot: A Simple Example
Computing the System Frequency Response from Difference Equation
System Frequency Response Examples
Wireless Connectivity Part 2. Classify Untethered Connection by Range, Tx Power, Date Rate & BW.
Everything You Need to Know About Frequency Response for Audio Gear!
Software Frequency Response Analyzer Hands-on Demo
Frequency response in 20-sim.
Natural Frequency, Resonance, and FRFs
T8V4-Derivation of the Frequency Response of an FIR Filter
Multisim Frequency Response Simulation
Frequency Response Example #2
Introduction to Frequency Response/Bode Plots for Dynamic Systems
15. Closed Loop Frequency Response
Intro to Control - 14.2 Frequency Response Example
Frequency Response Analyzer - Instrument Overview
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Solving for the Frequency Response of an LTI system from a Difference Equation
Beampattern: spatial frequency response
Control System Lectures - Bode Plots, Introduction
Комментарии
 0:16:43
0:16:43
 0:08:08
0:08:08
 0:20:53
0:20:53
 0:15:17
0:15:17
 0:08:02
0:08:02
 0:05:24
0:05:24
 0:06:52
0:06:52
 0:06:41
0:06:41
 0:29:47
0:29:47
 0:06:45
0:06:45
 0:08:13
0:08:13
 0:04:23
0:04:23
 0:07:42
0:07:42
 0:09:53
0:09:53
 0:07:33
0:07:33
 0:13:24
0:13:24
 0:35:22
0:35:22
 0:38:13
0:38:13
 0:09:13
0:09:13
 0:02:52
0:02:52
 0:00:16
0:00:16
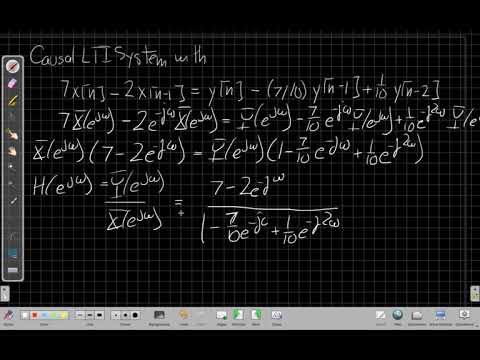 0:11:15
0:11:15
 0:08:26
0:08:26
 0:12:45
0:12:45