Lecture 18: Counting Parameters in SVD, LU, QR, Saddle Points

Показать описание

MIT 18.065 Matrix Methods in Data Analysis, Signal Processing, and Machine Learning, Spring 2018
Instructor: Gilbert Strang

In this lecture, Professor Strang reviews counting the free parameters in a variety of key matrices. He then moves on to finding saddle points from constraints and Lagrange multipliers.

License: Creative Commons BY-NC-SA

Рекомендации по теме

Комментарии

Dear Professor Strang, you and your lectures are more than gold. I just googled what the rarest and most precious metal is, and it turns out to be Palladium, so you and your lectures are pure Palladium!
Everything in the video is clearly explained, informative, clarifying and vastly illuminating. I'm excited about what is to come in next in the video lectures!
Bravo and applause

elyepes

DR. Strang thank you for counting and verifying the Parameters in SVD, LU, QR and Saddle Points in numerical linear algebra.

georgesadler

I love watching Prof Strang suddenly have an epiphany. It's like he wants to jump up and shout "Eureka!"

financeexplainedgraphics

@26:46: mr + nr - r^2 = mn - (m-r)(n-r) makes sense as all (mn) parameters of A less a redundant bit due to the low rank.

carl

Anybody found that there are no Ads in MIT OCW, wow!

allandogreat

Around 41:33, I think the number of pivots should be (n pos + m neg) pivots since A is a m by n matrix and (-A*inv(S)*A^T) is a m by m matrix.

RC.

@29:30, why does d/dx( L' (A x) ) become A' L? ( ' = transpose, L = lambda, d/dx = partial der.)

rogiervdw

Where can we get the notes of the class which are referred in the lecture so many times?

saketdwivedi

at 40:00, is the block elimination right? I guess [ I 0 : -A*inv(S) I]

kirinkirin

At 39:55, the professor multiply [A S-1] to the left side of [S AT; A 0] to get [S AT; 0 -A*S-1*AT]. Can anybody please explain the purpose of this calculation ? Thanks in advance!

shenzheng

at [46:30], he first said that the derivative of Rayleigh's quotient at the saddle points are zero, and it sounds like to me that he was recorrecting it by the eigenvectors, and how the values of the R(x) would be the eigenvalues. Can anybody shade some light? Thanks in advance.

vaghawanojha

Who knows for sure with deminsions. You do good to dream the Riemann.

brendawilliams

13:50 - it is a kind of reverse-engineering proof...

PrzemyslawSliwinski

Lecture 18: Counting Parameters in SVD, LU, QR, Saddle Points

Lecture 18: Counting Parameters in SVD, LU, QR, Saddle Points

Lecture 18: Counting Proper Colorings

Lecture 5.1 - Parameters in Verilog [English]

ECE4960 Lecture 18

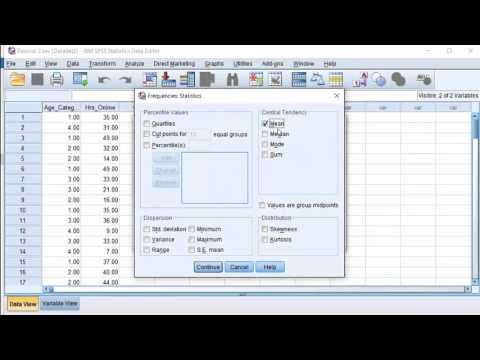
SPSS - Mean, Median, Mode, Standard Deviation & Range

[BayesCog] SoSe 2021 Lecture 10 - understanding parameters in the Rescorla-Wagner model

Lecture 18 -- Sensitivity Analyses [Agent-Based Modeling for Health Policy with AnyLogic]

Intro to ML Lecture 18 (Spring 2015)

Lecture 18 - Efficient Point Cloud Recognition | MIT 6.S965

IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit

DP 18. Count Partitions With Given Difference | Dp on Subsequences

Lecture 18: Measurement Techniques: Phase Fraction Measurement

Lecture 18B: Width Parameters, Auxiliary Variables and Extended Resolution

PGM 18Spring Lecture 8: Learning the parameters of UGM

Differential equations; Fall 2021; Lecture 18; Variation of parameters practice; systems of ODE

Lecture 18: HMMs Filtering

Lecture 18: Gluing Algorithms

Lecture 24: Estimating Parameters in Ordinary Differential Equations - Part 2

Lecture 18 Uniform and Exponential Random Variables

CS 354 Machine Organization and Programming Lecture 18 Iteration in Assembly

Lecture 18 - Topological Methods for the Analysis of Data

MAE 209 - Lecture 18 - The Normal Distribution and the Exponential Distribution - Winter 2022

23_AMC - Lecture 18

noc18-ce35-Lecture 20-Exercise on Morphometric Parameters