filmov
tv
Simplifying a Fun Radical Expression
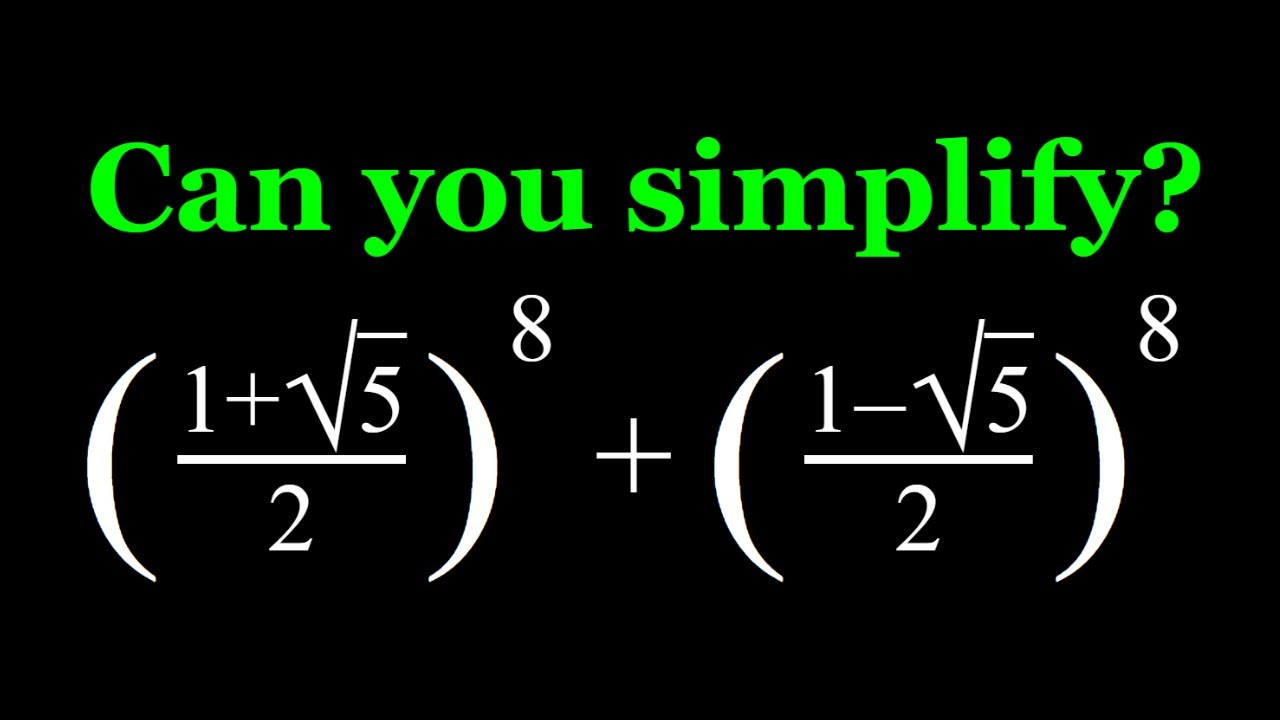
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalExpressions
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #RadicalExpressions
EXPLORE 😎:
PLAYLISTS 🎵 :
Simplifying a Fun Radical Expression
Simplify a radical expression with variables
Simplifying A Radical Expression
Simplifying A Nice Radical Expression
How to Simplify a Radical - The Fun Way
Simplifying Radical Expressions | 30 Examples
Interesting Ways to Simplify Radical Expressions | Algebra Fun
Germany | Can you solve this ? | Simplify Radical Expression
Math Olympiad |Find the value of 'X+Y' in this equation #youtubeshorts #sorts #sortvideo
A Nice Radical Problem | Simplifying Radical Expression With Division Of Negative Exponentes
Simplifying a Radical Expression with Clever Factoring, Part 1
Simplifying A Radical Expression The Hard Way
Simplify radical expressions #math #algebra #shorts #mathdrills #squareroot
Simplifying a Radical
5 simple unsolvable equations
Write into a Simplest Radical form | Fun Algebra Problem (9/4)^(9/4) | College Entrance Exam
Math Trick - How to simplify a double-layer radical expression in only 1 minute?
Simplifying radical expressions
Calculators NOT allowed | Fun Algebra Problem | Radical with rational exponents
Simplifying Radical Expressions
Radical Simplification #shorts #maths #radical #simplification #mathpractice
A Nice Radical Problem | Simplify Radical Expression
When mathematicians get bored (ep1)
Solve and simplify this radical expression. Math Olympiad Algebra Problem.
Комментарии
 0:05:14
0:05:14
 0:05:14
0:05:14
 0:00:51
0:00:51
 0:00:39
0:00:39
 0:02:52
0:02:52
 0:45:59
0:45:59
 0:14:01
0:14:01
 0:10:20
0:10:20
 0:01:00
0:01:00
 0:02:36
0:02:36
 0:00:58
0:00:58
 0:00:42
0:00:42
 0:00:13
0:00:13
 0:00:28
0:00:28
 0:00:50
0:00:50
 0:03:41
0:03:41
 0:02:07
0:02:07
 0:00:39
0:00:39
 0:04:52
0:04:52
 0:35:45
0:35:45
 0:00:50
0:00:50
 0:09:32
0:09:32
 0:00:37
0:00:37
 0:02:25
0:02:25