filmov
tv
Vectors 18 • Shortest Distance between Parallel Planes - Parametric Form • CP1 Ex9F • 🎯

Показать описание
Edexcel Core Pure Year 1
Mon 9/3/20
Mon 9/3/20
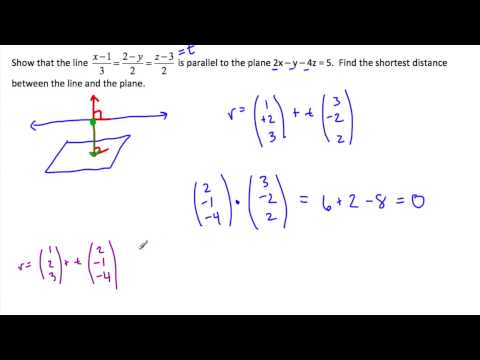
Vectors 18 • Shortest Distance between Parallel Planes - Parametric Form • CP1 Ex9F • 🎯
Calculus 3: Ch 2.1 Lines and Vectors in 3-D (18 of 20) Shortest Distance Between 2 Lines in 3-D
Vector Planes Ex11 - Shortest distance line and plane
VECTORS TEST: Shortest Distance of a Point from Symmetric Line Equation
18 Find Shortest Distance of Line from Origin
Find a Point on a Vector Planes at the Shortest Distance from a Point
VECTORS Shortest Distance from Point to Plane with Cross Product
Foot of the Perpendicular and Shortest Distance from Point Vectors Line
ENGR 213 Lecture 13: Cross Products of Two Vectors, A × B (2024.09.18)
Shortest Distance Between a Line and a Plane - Linear Algebra
[A Level Further Math] Vectors | Part 3 | Further Pure Mathematics 1
Distance between two skew lines Vectors 2016 Test
Calculus 3: Ch 2.1 Lines and Vectors in 3-D (17 of 20) Shortest Distance Between 2 Lines 2-D
Shortest Distance Between Skew Lines
Position vector for a boat with given speed and direction and shortest distance from port
A-Level Further Maths F5-04 Intersections: Finding the Distance between two Parallel Lines
VECTORS Shortest Distance From a Point to Line in Three Space MCV4U Two Methods Dot Cross Products
Vectors 6 Part 05: Shortest distance bet point and line
Shortest Distance Between Skew Lines with Parametric Equations
A-Level Further Maths F6-18 Vector Product: Distance from a Point to a Line in 2D Exploration
Vectors 17 • Shortest Distance between Plane and Point/Parallel Planes • CP1 Ex9F • 🎯
Shortest distance between boat and a point Vector Velocity Application
A-Level Further Maths F6-15 Vector Product: Distance from a Point to a Line in 3D Exploration
Foot of Perpendicular and Shortest Distance Vector R3 Q9
Комментарии
 0:01:52
0:01:52
 0:07:21
0:07:21
 0:05:34
0:05:34
 0:04:50
0:04:50
 0:06:03
0:06:03
 0:07:58
0:07:58
 0:17:50
0:17:50
 0:08:11
0:08:11
 0:45:28
0:45:28
 0:11:26
0:11:26
 0:21:48
0:21:48
 0:05:52
0:05:52
 0:03:34
0:03:34
 0:12:26
0:12:26
 0:17:21
0:17:21
 0:05:49
0:05:49
 0:20:48
0:20:48
 0:10:02
0:10:02
 0:02:49
0:02:49
 0:06:40
0:06:40
 0:09:30
0:09:30
 0:14:50
0:14:50
 0:09:15
0:09:15
 0:08:20
0:08:20