filmov
tv
GADEPs focused conference: Abelian and iterated integrals and Hilbert 16th problem - J. Pontigo
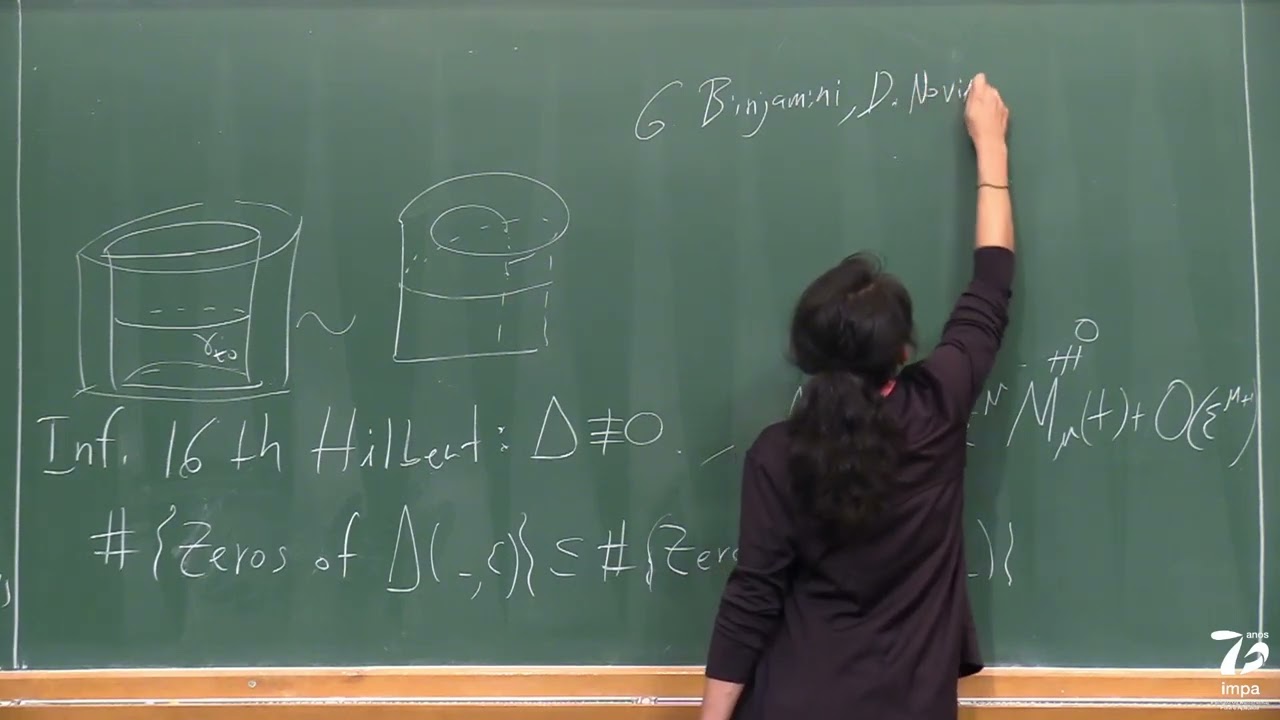
Показать описание
IMPA, Rio de Janeiro, 26-30 September 2022
Speaker: J. Pontigo - TBA
The seminar “Geometry, Arithmetic and Differential Equations of Periods” (GADEPs), started in the pandemic year 2020 and its aim is to gather people in different areas of mathematics around the notion of abelian integrals and periods which are certain multiple integrals. This is the first GADEPs conference focused on Hilbert 16th problem. It asks on the uniform bound for the number of limit cycles of planar differential equations, and it is still challenging even for quadratic differential equations. Attempts to approach this conjecture have given origin to many results in holomorphic foliations on complex surfaces and classification of their singularities. The birth of limit cycles after a perturbation of foliations with a first integral is controlled by the zeros of abelian integrals which are the first Melnikov functions of the deformed holonomy map (Poincaré first return map). The infinitesimal Hilbert 16th problem asks for finding a realistic bound for the number of zeros of abelian integrals, and attempts to understand this, have produced many results in Picard-Lefschetz theory of fibrations and Picard-Fuchs equations. When an abelian integral is identically zero, higher Melnikov functions are expressed as Chen’s iterated integrals and their study is closely related to the topology of leaves of holomorphic foliations near to those with a first integral. The conference main core will consist of 5 lecture series which aim to introduce main methods and conjectures of the topic to a broad public and in particular graduate students.
The conference will be in hybrid format and it will be transmitted through IMPA’s YouTube channel.
Organizers:
Hossein Movasati (IMPA)
Younes Nikdelan (UERJ)
Suely Lima (IMPA)
IMPA - Instituto de Matemática Pura e Aplicada ©
Os direitos sobre todo o material deste canal pertencem ao Instituto de Matemática Pura e Aplicada, sendo vedada a utilização total ou parcial do conteúdo sem autorização prévia e por escrito do referido titular, salvo nas hipóteses previstas na legislação vigente.
The rights over all the material in this channel belong to the Instituto de Matemática Pura e Aplicada, and it is forbidden to use all or part of it without prior written authorization from the above mentioned holder, except in the cases prescribed in the current legislation.
Speaker: J. Pontigo - TBA
The seminar “Geometry, Arithmetic and Differential Equations of Periods” (GADEPs), started in the pandemic year 2020 and its aim is to gather people in different areas of mathematics around the notion of abelian integrals and periods which are certain multiple integrals. This is the first GADEPs conference focused on Hilbert 16th problem. It asks on the uniform bound for the number of limit cycles of planar differential equations, and it is still challenging even for quadratic differential equations. Attempts to approach this conjecture have given origin to many results in holomorphic foliations on complex surfaces and classification of their singularities. The birth of limit cycles after a perturbation of foliations with a first integral is controlled by the zeros of abelian integrals which are the first Melnikov functions of the deformed holonomy map (Poincaré first return map). The infinitesimal Hilbert 16th problem asks for finding a realistic bound for the number of zeros of abelian integrals, and attempts to understand this, have produced many results in Picard-Lefschetz theory of fibrations and Picard-Fuchs equations. When an abelian integral is identically zero, higher Melnikov functions are expressed as Chen’s iterated integrals and their study is closely related to the topology of leaves of holomorphic foliations near to those with a first integral. The conference main core will consist of 5 lecture series which aim to introduce main methods and conjectures of the topic to a broad public and in particular graduate students.
The conference will be in hybrid format and it will be transmitted through IMPA’s YouTube channel.
Organizers:
Hossein Movasati (IMPA)
Younes Nikdelan (UERJ)
Suely Lima (IMPA)
IMPA - Instituto de Matemática Pura e Aplicada ©
Os direitos sobre todo o material deste canal pertencem ao Instituto de Matemática Pura e Aplicada, sendo vedada a utilização total ou parcial do conteúdo sem autorização prévia e por escrito do referido titular, salvo nas hipóteses previstas na legislação vigente.
The rights over all the material in this channel belong to the Instituto de Matemática Pura e Aplicada, and it is forbidden to use all or part of it without prior written authorization from the above mentioned holder, except in the cases prescribed in the current legislation.
 0:49:39
0:49:39
 0:59:51
0:59:51
 0:53:51
0:53:51
 0:55:38
0:55:38
 0:55:35
0:55:35
 0:57:17
0:57:17
 1:07:38
1:07:38
 0:51:53
0:51:53
 1:06:07
1:06:07
 1:00:58
1:00:58
 0:41:28
0:41:28
 0:53:52
0:53:52
 1:05:09
1:05:09
 0:52:56
0:52:56
 1:15:56
1:15:56
 0:42:32
0:42:32
 0:58:50
0:58:50
 0:35:41
0:35:41
 0:45:56
0:45:56
 0:53:13
0:53:13
 0:51:20
0:51:20
 0:59:05
0:59:05
 1:01:21
1:01:21
 1:00:11
1:00:11