🌀U Can't Guess it's shape-|desmos|-infinitym4th

#desmos #art #parametric #mathart #graphing

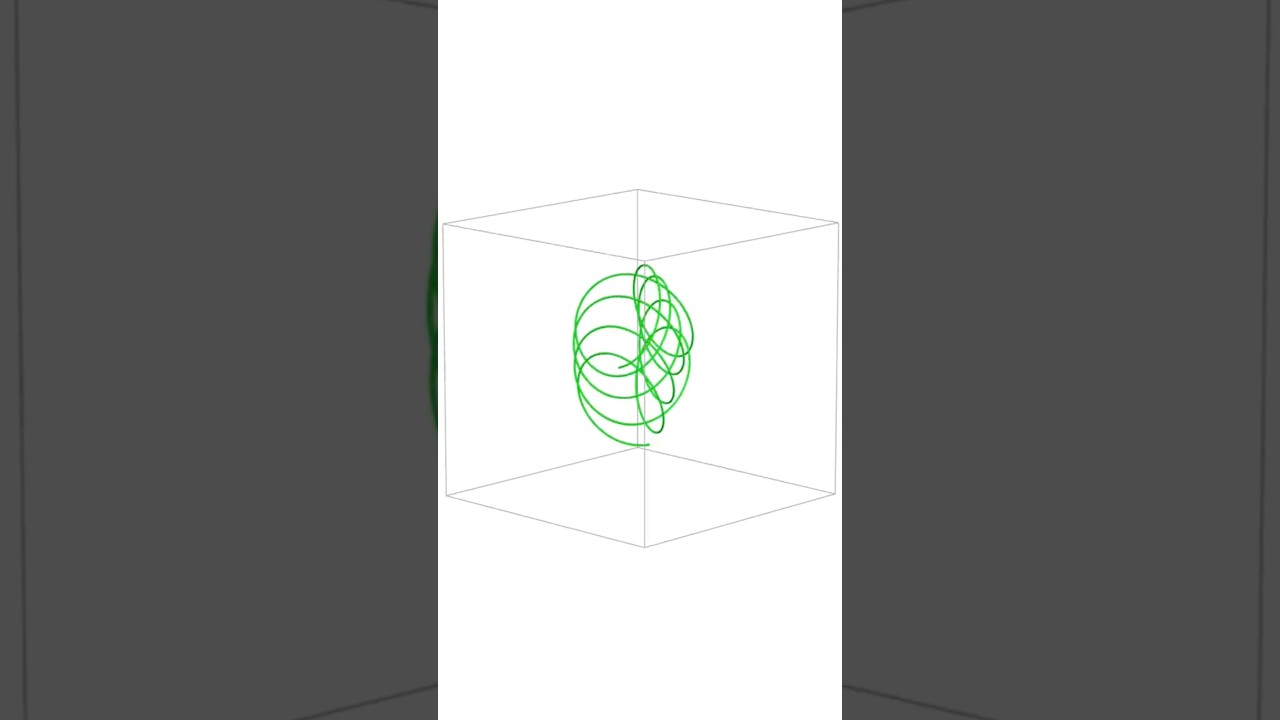
Parametric equations offer a fascinating way to describe curves by expressing the coordinates of points as functions of an independent variable, typically time. When these equations are crafted with specific periodic functions like sine and cosine, they generate intricate, flowing shapes that can appear to have depth and motion, even in 2D space.

By manipulating parameters such as frequency, amplitude, and phase shifts, the equations create paths that intertwine, loop, and twist, creating an illusion of 3D motion. These curves can simulate the dynamic flow of movement, as the x and y coordinates evolve over time, often giving the impression of spinning, rotation, or folding in space.

This visual illusion happens because the human brain interprets the overlapping and curvature of the lines as depth cues, much like how we perceive real-world objects in motion. As a result, parametric equations can be used to generate shapes that resemble complex physical systems like orbits, waves, or even abstract geometric art that seems to shift and move before our eyes. These equations beautifully blend mathematics, art, and motion, making them a powerful tool for creating visually striking and engaging simulations.