Set Theory Proof: Prove that if A union B is Empty then A is Empty of B is Empty

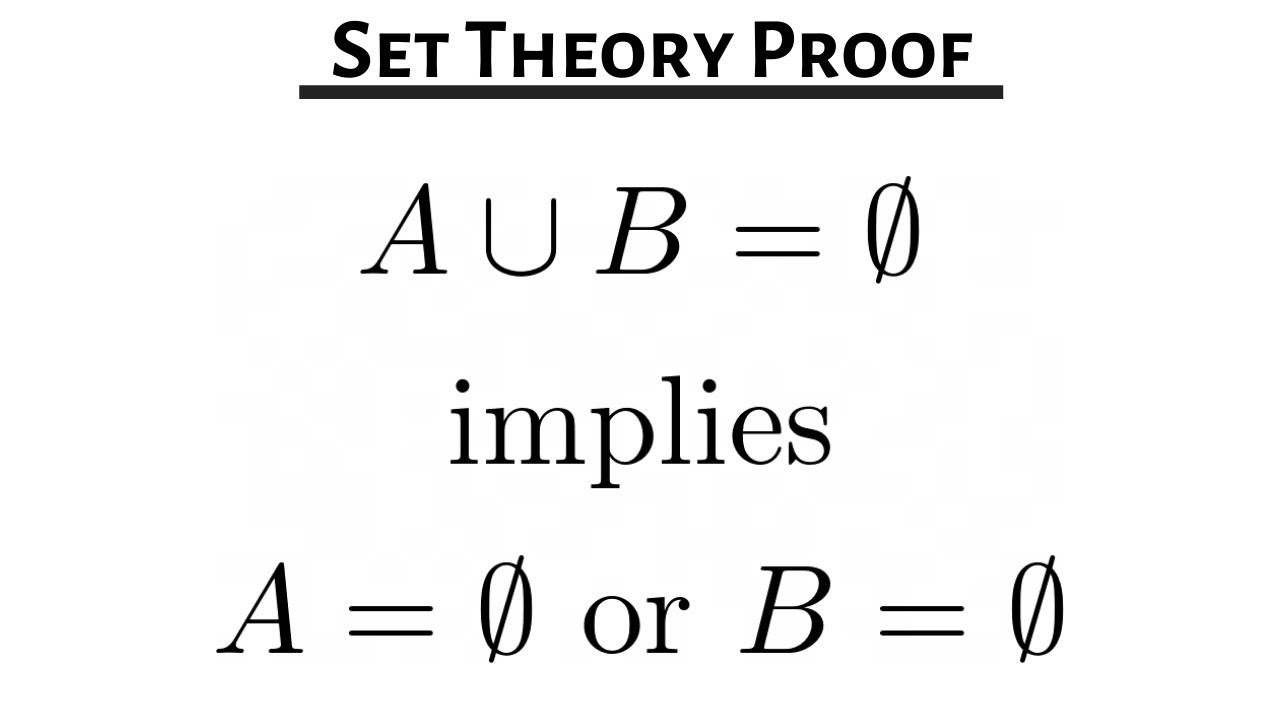
preview_player
Показать описание
Set Theory Proof: Prove that if A union B is Empty then A is Empty of B is Empty

If you enjoyed this video please consider liking, sharing, and subscribing.

There are several ways that you can help support my channel:)

************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course

Advanced Calculus Course

Calculus 1 Course

Calculus 2 Course

Calculus 3 Course

Calculus Integration Insanity

Differential Equations Course

College Algebra Course

How to Write Proofs with Sets Course

How to Write Proofs with Functions Course

Statistics with StatCrunch Course

Math Graduate Programs, Applying, Advice, Motivation

Daily Devotionals for Motivation with The Math Sorcerer

Thank you:)
  1. The Math Sorcerer
  2. proof with sets
  3. set theory
  4. proof
  5. sets
  6. math proof with sets
Рекомендации по теме
How to do 0:16:30

How to do a PROOF in SET THEORY - Discrete Mathematics

Set Theory Proof: 0:07:58

Set Theory Proof: Prove that the Relative Complement Distributes over the Intersection of Sets

Set Theory Proof 0:03:04

Set Theory Proof with the Math Sorcerer

Set Theory Proof 0:05:39

Set Theory Proof A is a subset of B if and only if A intersect B = A

Set Theory Proof 0:02:05

Set Theory Proof Example

Proving Sets 0:22:12

Proving Sets

Set Theory Proof 0:03:44

Set Theory Proof with Complements

Set Theory Proof 0:04:55

Set Theory Proof | Prove that A ∩ ( B ∪ C ) = (A ∩ B) ∪ (A ∩ C) | Discrete Math

ICMAM Latin America 0:56:44

ICMAM Latin America 2024 - Day 3, part 2

Set Theory Subset 0:03:45

Set Theory Subset Proof

Using Set Properties 0:04:56

Using Set Properties prove set equality. Set Theory. Abstract Algebra

Prove A is 0:06:36

Prove A is a subset of B with the ELEMENT METHOD

Set Theory | 0:29:24

Set Theory | All-in-One Video

Discrete Math - 0:17:49

Discrete Math - 2.2.3 Proving Set Identities

Prove De Morgan's 0:03:37

Prove De Morgan's Law in Set Theory Complement of Union is Intersection of Complements

Set Theory Proof: 0:03:44

Set Theory Proof: If A n B = empty! then A is a subset of B complement

Proof of the 0:03:15

Proof of the Distributive Law for Sets

How to Prove 0:06:55

How to Prove Two Sets are Equal using the Method of Double Inclusion A n (A u B) = A

Proving subsets 0:06:43

Proving subsets

Proving equalities of 0:03:01

Proving equalities of sets using the element method

Set Theory Proof 0:01:59

Set Theory Proof (A\B) n B = Empty!

Set Theory Proof: 0:02:26

Set Theory Proof: Prove that if A union B is Empty then A is Empty of B is Empty

Basic Set Theory: 0:03:36

Basic Set Theory: Proof of the transitivity of the subset relation.

Direct Proof: Prove 0:03:54

Direct Proof: Prove that if 5x - 7 is odd, then 9x + 2 is even

Комментарии
Автор

Is that for AUB=empty, then set A and set B must both be empty. Instead of A= empty or B=empty.

phkw
Автор

I think i got it,
If A=phi OR B= phi, then
It means
A= phi AND B not equal OR
A not equal phi AND B= OR
A= phi AND B=


In above 3rd statement is actually correct for A U B= phi but it is in OR with Statement 1 and 2 so statement 4 is valid for A U B= phi.

Iam i correct?

Marshall...-_-
Автор

but I wonder why A=phi or B=phi it be A=phi and B=phi.... isn't A union phi=A and
phi union understand proof is right but I feel some confusion....can you clarify it please?

mahmoudalbahar
Автор

Really nice vedio about set theory i started to understand it when i started watsh your vedio 👍

mahmoudmroweh