filmov
tv
General Relativity Lecture 4: Spacetimes, SO(1,3), Spacetime Diagrams and Causality
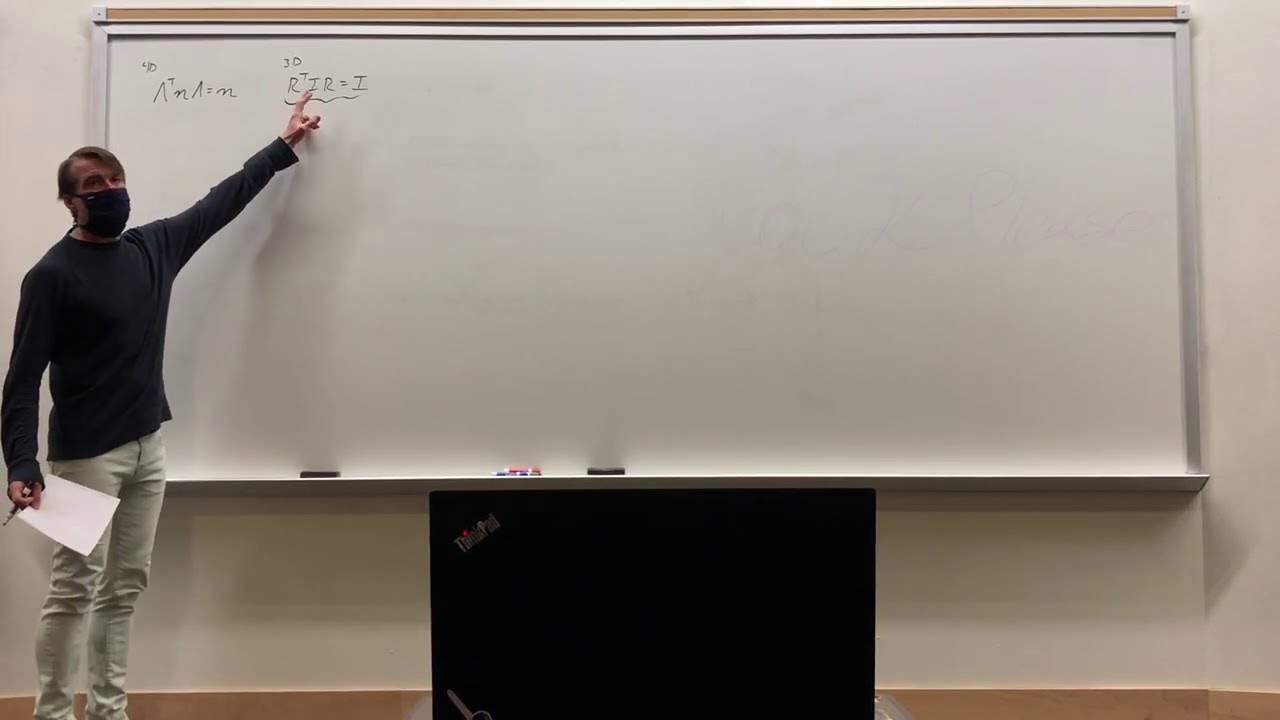
Показать описание
Lecture from 2021 senior/graduate level course in general relativity in physics at Colorado School of Mines. You can follow along at:
General Relativity Lecture 4: Spacetimes, SO(1,3), Spacetime Diagrams and Causality
General Relativity Lecture 4
General Relativity Topic 4: Spacetimes, SO(1,3), Spacetime Diagrams and Causality
Introduction to mass and energy in general relativity - Lecture 4
The cosmic censorship conjectures in general relativity - Lecture 4
4. Special Relativity (General Relativity)
David Fajman: Dynamics of General Relativity 4
PHS3131 Special Relativity Lecture 4 David Paganin
Lecture 4 Advanced General Relativity Eric Poisson 2024
Lecture #4 : General Relativity | Lorentz transformation
Greg Galloway: Topology & General Relativity 4
Relativity 107e: General Relativity Basics - Stress-Energy-Momentum Tensor
Special Relativity | Lecture 4
What is General Relativity? Lesson 25: The Geodesics of Schwarzschild spacetime Part 4
What is General Relativity? Lesson 22: The geodesics of the Schwarzschild spacetime
General Relativity Explained simply & visually
General theory of relativity | General relativity explained | General relativity lecture
General relativity | General relativity explained | Einstein field equations explained | Geodesics
General Relativity: Lecture 7: 4-vectors and physics in Special Relativity
General Relativity Lecture 4 Dr. Sunandan Gangopadhyay
General Relativity Lecture 4 Dr Sunandan Gangopadhyay
General Relativity, Lecture 4
SH2372 General Relativity - Lecture 4
Relativity 107d: General Relativity Basics - Curved Spacetime for Newtonian Gravity (Newton Cartan)
Комментарии
 1:08:23
1:08:23
 1:41:02
1:41:02
 1:08:47
1:08:47
 1:10:14
1:10:14
 1:20:40
1:20:40
 0:54:58
0:54:58
 0:37:35
0:37:35
 0:50:04
0:50:04
 1:21:00
1:21:00
 0:24:57
0:24:57
 0:43:54
0:43:54
 0:34:07
0:34:07
 1:50:11
1:50:11
 0:35:12
0:35:12
 0:45:19
0:45:19
 0:14:04
0:14:04
 0:38:15
0:38:15
 0:49:36
0:49:36
 0:55:18
0:55:18
 1:41:16
1:41:16
 1:41:16
1:41:16
 1:48:17
1:48:17
 1:16:06
1:16:06
 0:25:13
0:25:13