filmov
tv
Worked example: Approximation with local linearity | AP Calculus AB | Khan Academy

Показать описание
Finding the equation of a tangent line at a point of a curve by knowing the derivative at that point. Then using that equation to approximate the value of the function at close by x-values.
AP Calculus AB on Khan Academy: Bill Scott uses Khan Academy to teach AP¨_ Calculus at Phillips Academy in Andover, Massachusetts, and heÕs part of the teaching team that helped develop Khan AcademyÕs AP¨_ lessons. Phillips Academy was one of the first schools to teach AP¨_ nearly 60 years ago.
Khan Academy is a nonprofit organization with the mission of providing a free, world-class education for anyone, anywhere. We offer quizzes, questions, instructional videos, and articles on a range of academic subjects, including math, biology, chemistry, physics, history, economics, finance, grammar, preschool learning, and more. We provide teachers with tools and data so they can help their students develop the skills, habits, and mindsets for success in school and beyond. Khan Academy has been translated into dozens of languages, and 15 million people around the globe learn on Khan Academy every month. As a 501(c)(3) nonprofit organization, we would love your help! Donate or volunteer today!
Комментарии
 0:03:35
0:03:35
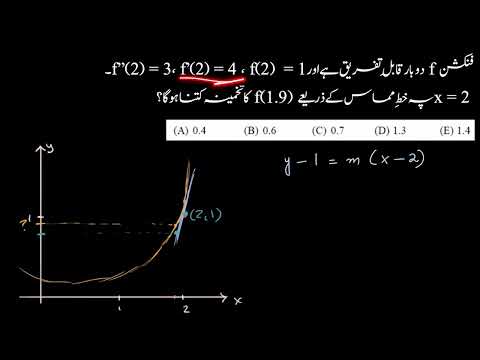 0:01:49
0:01:49
 0:00:33
0:00:33
 0:05:31
0:05:31
 0:04:16
0:04:16
 0:13:12
0:13:12
 0:00:54
0:00:54
 0:13:48
0:13:48
 5:46:00
5:46:00
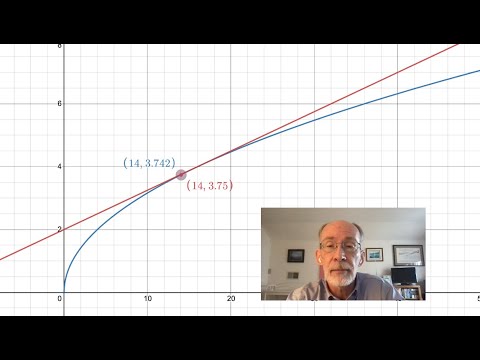 0:08:49
0:08:49
 0:01:00
0:01:00
 0:13:23
0:13:23
 0:01:51
0:01:51
 0:19:09
0:19:09
 0:02:51
0:02:51
 0:09:38
0:09:38
 0:44:38
0:44:38
 0:11:49
0:11:49
 0:00:38
0:00:38
 0:59:22
0:59:22
 0:04:56
0:04:56
 0:04:37
0:04:37
 0:15:36
0:15:36
 0:03:07
0:03:07