filmov
tv
Philippines Maths Olympiad 2020 Problem | Geometry | Important Geometry Skills Explained
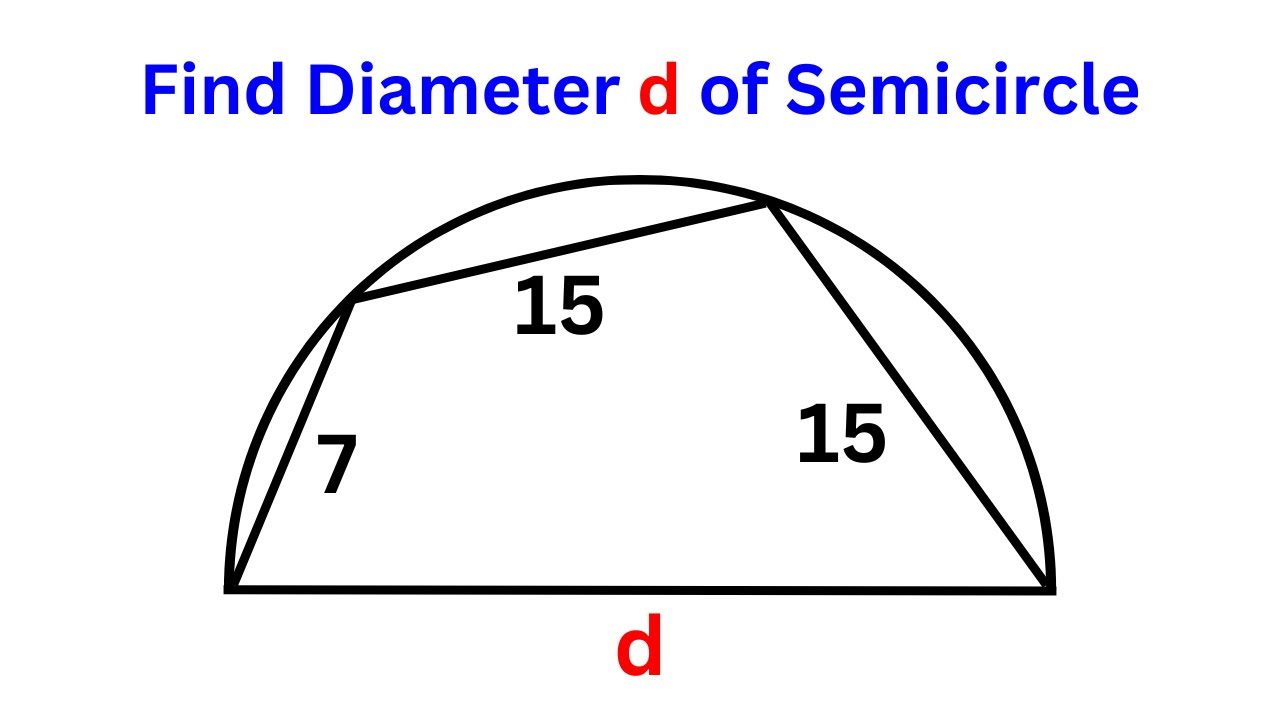
Показать описание
Philippines Maths Olympiad 2020 Problem | Geometry | Important Geometry Skills Explained
Join this channel to get access to perks:
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
Sambasivam Sathyamoorthy
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Saunak Swar
Join this channel to get access to perks:
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
Sambasivam Sathyamoorthy
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Saunak Swar
Philippines Maths Olympiad 2020 Problem | Number Theory
Philippines Maths Olympiad 2020 Problem | Geometry | Important Geometry Skills Explained
Philippines Maths Olympiad 2020 Problem | Algebra | 2 Different Methods
Philippines Maths Olympiad 2020 Problem | PMO 2020 | Mathematics
Philippines Mathematical Olympiad 2020 | Philippines maths Olympiad #olympiad #philippines #imo
Philippines Maths Olympiad 2020 Problem | PMO | Number Theory
800. “Philippines Maths Olympiad 2020 Problem'
A Challenging Number Theory Problem From Philippines Math Olympiad 2020
Philippines Math Olympiad |Philippines Mathematical Olympiad Question #olympiad #imo #philippines
Philippine Mathematical Olympiad | Can you solve this interesting Math Problem
Philippine Mathematical Olympiad (PMO) 2020 Qualifying Stage #1–3
Math Olympiad Question | You should know how to solve this!!
Philippine Math Olympiad Problem
How to solve the Philippine Math Olympiad Questions - Olympiad Tutorial
Selected Questions of Philippines Maths Olympiad 2020 | Maths Olympiad 2021-22 | Abhay Sir | VOS
Philippines Math Olympiad | Philippines Mathematical Olympiad Question #imo #olympiad #philippines
Luxembourg - Math Olympiad Question | You should know this trick
Math Olympiad Problem Solving No. 1 (10th Philippine Math Olympiad) I Earl Brian Roble
PMO2 2022 problem2 solutions 24th national stage written phase day1 philippine mathematical olympiad
Philippine Mathematical Olympiad (PMO) 2020 Qualifying Stage #13
PH Math Olympiad 2019 Finals: Summation with Totient
Philippine Mathematical Olympiad 2020-2021
Young lady absolutely kills it in Nigerian Maths Competition!
Math Olympiad question | Philippines Math Olympiad | 2 semicircles
Комментарии
 0:09:53
0:09:53
 0:14:22
0:14:22
 0:16:47
0:16:47
 0:06:39
0:06:39
 0:04:52
0:04:52
 0:06:04
0:06:04
 0:01:23
0:01:23
 0:12:30
0:12:30
 0:04:50
0:04:50
 0:03:20
0:03:20
 0:05:47
0:05:47
 0:02:24
0:02:24
 0:06:26
0:06:26
 0:06:25
0:06:25
 1:38:07
1:38:07
 0:06:49
0:06:49
 0:02:51
0:02:51
 0:08:12
0:08:12
 0:11:10
0:11:10
 0:03:47
0:03:47
 0:14:27
0:14:27
 0:03:02
0:03:02
 0:01:35
0:01:35
 0:04:38
0:04:38