filmov
tv
Integral of 1/(1 + sinx) ❖ Calculus 1 ❖ Trig Integrals
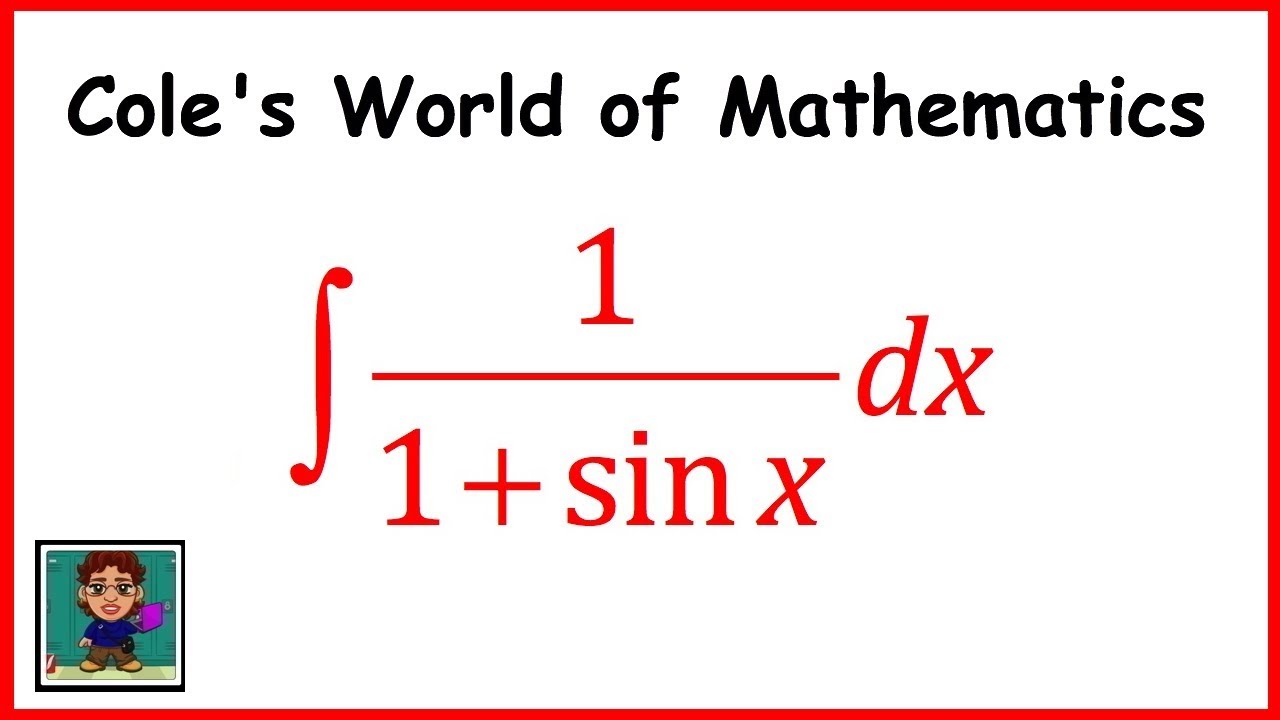
Показать описание
This video goes through the integral of 1/(1 + sinx). This type of integral is typically found in a Calculus 1 class.
*******************************************
Math Tutorials on this channel are targeted at college-level mathematics courses including calculus, pre-calculus, college algebra, trigonometry, probability theory, TI-84 tutorials, introductory college algebra topics, and remedial math topics from algebra 1 and 2 for the struggling college adult (age 18 and older).
*******************************************
Don’t forget guys, if you like this video please “Like” and “Share” it with your friends to show your support - it really helps me out!
*******************************************
*******************************************
Interested in purchasing the TI-84 Plus CE Graphing Calculator?
*******************************************
Be sure to Check Out Cole’s World of Mathematics Merchandise!
Supporting Cole’s World of Mathematics is as easy as 1-2-3.
*******************************************
For More Math Tutorial Videos, check out all of my Playlists:
*******************************************
Be sure to check out Cole’s World of Mathematics around the web!
*******************************************
DISCLAIMER: This video description contains affiliate links, which means that if you click on one of the product links, I’ll receive a small commission. This helps support the channel and allows me to continue to make videos like this. Thank you for the support!
*******************************************
*******************************************
Math Tutorials on this channel are targeted at college-level mathematics courses including calculus, pre-calculus, college algebra, trigonometry, probability theory, TI-84 tutorials, introductory college algebra topics, and remedial math topics from algebra 1 and 2 for the struggling college adult (age 18 and older).
*******************************************
Don’t forget guys, if you like this video please “Like” and “Share” it with your friends to show your support - it really helps me out!
*******************************************
*******************************************
Interested in purchasing the TI-84 Plus CE Graphing Calculator?
*******************************************
Be sure to Check Out Cole’s World of Mathematics Merchandise!
Supporting Cole’s World of Mathematics is as easy as 1-2-3.
*******************************************
For More Math Tutorial Videos, check out all of my Playlists:
*******************************************
Be sure to check out Cole’s World of Mathematics around the web!
*******************************************
DISCLAIMER: This video description contains affiliate links, which means that if you click on one of the product links, I’ll receive a small commission. This helps support the channel and allows me to continue to make videos like this. Thank you for the support!
*******************************************
Комментарии
 0:03:46
0:03:46
 0:03:35
0:03:35
 0:04:51
0:04:51
 0:00:37
0:00:37
 0:04:12
0:04:12
 0:00:52
0:00:52
 0:02:34
0:02:34
 0:00:45
0:00:45
 5:47:36
5:47:36
 0:03:27
0:03:27
 0:05:58
0:05:58
 0:05:21
0:05:21
 0:02:04
0:02:04
 0:01:20
0:01:20
 0:06:41
0:06:41
 0:02:32
0:02:32
 0:02:58
0:02:58
 0:06:24
0:06:24
 0:05:03
0:05:03
 0:06:29
0:06:29
 0:02:58
0:02:58
 0:00:21
0:00:21
 0:05:12
0:05:12
 0:02:11
0:02:11