filmov
tv
Why do squares and circles both have 360 degrees?

Показать описание
Why do squares and circles both have 360 degrees?
Why are Squares and Circles so important in Up animation? 🤔
4 Squares 1 Circle
Why is a Circle 360 Degrees, Why Not a Simpler Number, like 100?
All these squares make a circle
#PHUTURENOIZE #DEFQON1 . .PHUTURE NOIZE -- CIRCLES & SQUARES ( Defqon1) live
Dolphin Readers - Level 2 - Circles and Squares
Area of the Shaded Region Using Squares & Circles | SAT Math | JusticeTheTutor #maths #math #sho...
Hard SAT Math Question YOU Must Know! - Geometry of Circles (2024)
Circles, Triangles, Squares / English version
All these squares make a circle (TADC animation)
Circles are Squares in Dnd 5e
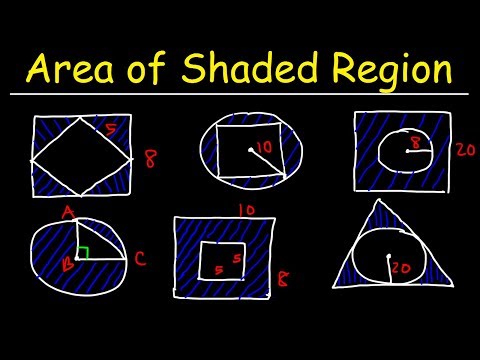
Area of Shaded Region - Circles, Rectangles, Triangles, & Squares - Geometry
Squares inside circle problem | Radius of circle | Advanced math problems | Mathematics
Circle or Squares? An Interesting Illusion
Squares inside circle problem | Radius of circle | Advanced math problems | Mathematics
Circles, Squares, Triangles, and Rectangles | Learning Shapes | Khan Academy Kids
Animation of Circles and Squares by Bo Burnham
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
Are You Funct!onal? (About Squares & Circles)
A Circle With 4 Squares
squares vs circles #sad
Rocko - Squares out your Circle ft Future (OFFICIAL VIDEO)
Circles Are Squares
Комментарии
 0:01:40
0:01:40
 0:00:45
0:00:45
 0:04:58
0:04:58
 0:03:54
0:03:54
 0:03:02
0:03:02
 0:01:56
0:01:56
 0:02:33
0:02:33
 0:00:45
0:00:45
 0:12:03
0:12:03
 0:05:29
0:05:29
 0:00:30
0:00:30
 0:01:00
0:01:00
 0:13:36
0:13:36
 0:06:12
0:06:12
 0:02:19
0:02:19
 0:00:36
0:00:36
 0:00:38
0:00:38
 0:00:22
0:00:22
 0:22:10
0:22:10
 0:08:25
0:08:25
 0:04:05
0:04:05
 0:00:56
0:00:56
 0:04:34
0:04:34
 0:00:50
0:00:50