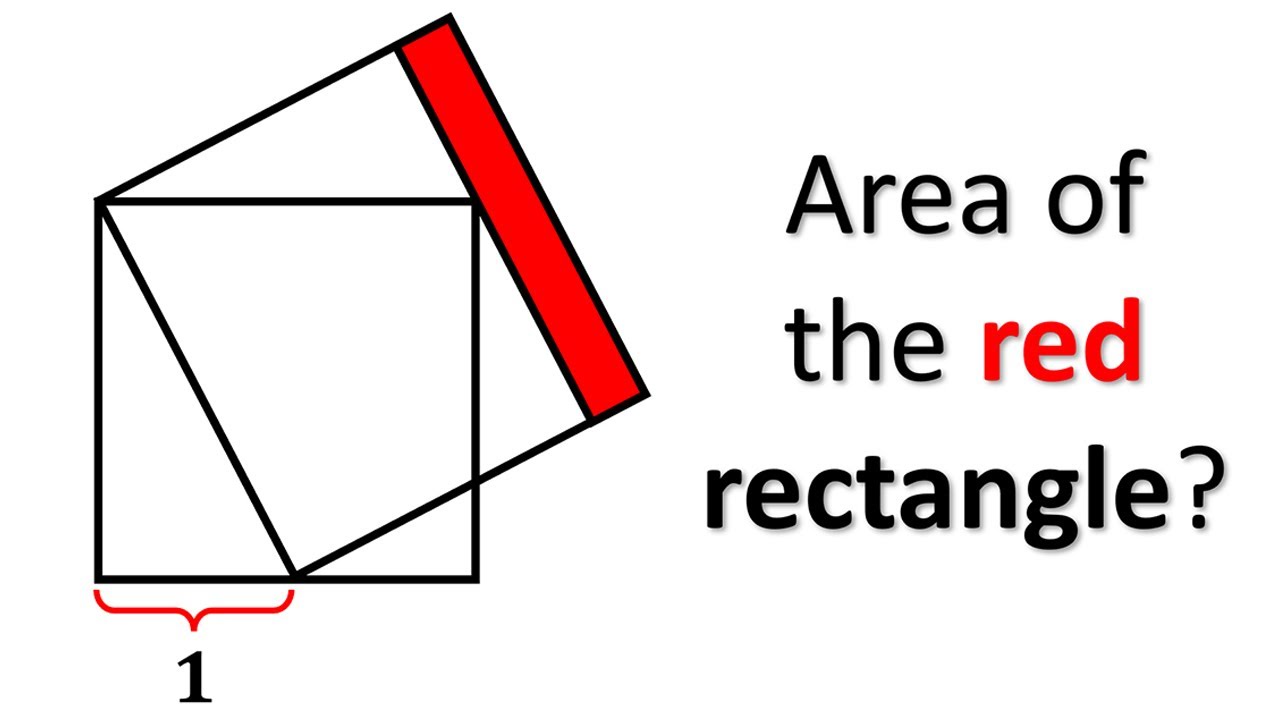
Calculate the Area of the Red Rectangle

In today's video, we'll tackle an intriguing geometry problem: calculating the area of the red rectangle. This problem might seem simple at first, but it requires a good understanding of geometric principles.

🔍 In this video, you will learn:
- How to identify key elements of the given shape.
- Step-by-step instructions to calculate the area of the red rectangle.
- Useful tips and tricks to solve similar geometry problems.

📐 Topics Covered:
- Basic geometric shapes and properties
- Area calculation techniques
- Problem-solving strategies in geometry

Don't forget to:
- Like the video if you found it helpful 👍.
- Subscribe to our channel for more math tutorials and problem-solving tips.
- Hit the bell icon 🔔 to get notified whenever we post new content.

Have questions or suggestions? Drop them in the comments below. I love hearing from you!

-------------------------------------------------------------------
📧 Contact Me:
------------------------------------------------------------------

Happy learning and see you in the video!

[ClassicalMusicFan]

a straightforward way, with only 1 unknown, a :
Stop at 1:43.
In ΔADE, DE=sqrt(1+a^2).
∠ADE=∠PDC, hence ΔADE~ΔPDC and DE/DC=AD/PD. We get PD=a^2/(sqrt(1+a^2)).
Now, the answer=area DEFG - area DEQP = DE^2 - DE⋅PD= 1.

[caperider]

Your second solution was inspirational! It opened my eyes to the deeper truth within the problem which I did not see at first. And wouldn't have seen it at all. So this ratio is regardless of the actual sizes of the squares. I also solved the problem but my method was basically the same approach as your first solution.

How does one develop such intuition?? Please tell me something.

[romain.guillaume]

Area is 1.

Set x the side of the small triangle.

From the Gogu theorem we get the side of the inclined square : sqrt(1+x2) = y

Let z be the distance from the top left corner to the intersection point between the top side of the inclined square and the constructed parallel line.

Because the bottom left right triangle is similar to the top right angle triangle of hypotenuse x (same two angles), we can write :
z/x = x/y

Solving for z with respect to x we get:

z = x2/sqrt(1+x2)

The area we are interested in is :
A = y*(y-z) which simplifies quickly to 1 after replacing y and z with our previous formulas.

[Hogscraper]

I got the same answer but got it just before the need to recognize that the short side of the red rectangle was 1/2 of the area of the large square. By that point it was already obvious that the large square has area 2 and half the small square, (two of the triangles together), have area .5. Once you see that all of the small triangles are congruent you can just double that and subtract, 2-1=1. Interesting problem with the different ways it can work out.

[santiagoarosam]

Respetando las premisas del trazado de la figura propuesta podemos suponer, sin alterar el resultado final, que el cuadrado original es de dimensiones √3*√3→ El cuadrado grande estará girado 30º respecto al inicial y tendrá dimensiones 2*2→ El triángulo cuya hipotenusa es el lado superior del cuadrado inicial tendrá un cateto largo de longitud (√3√3/2=3/2)→ Área del rectángulo rojo =(2*2)-[(3/2)*2] =4-3=1 ud².
Interesante problema. Gracias y un saludo cordial.

[andrewclifton]

Area = 1. My reasoning is as follows.

Suppose the small square has side (1 + x) and the large square has side y. Pythagoras using the triangle at the left side of the diagram, tells us that 1^2 + (1 + x)^2 = y^2. The rectangle with sides y and z - in other words the piece of the large square which is not red - has area yz; so the area of the red rectangle is y^2 - yz.

The triangle at the left formed by the sides of the two squares, and the triangle at the top formed by the edge of the small square and the part edge of the large square are similar. Looking at side ratios of these two triangles and comparing the hypotenuse to the longer side

y / (1 + x) = (1 + x) / z

Multiply out gives

yz = (1 + x)^2

So the area of the red rectangle is y^2 - yz

We know that y^2 = 1 + (1+x)^2, and we know that yz = (1 + x)^2

So the area of the red rectangle is 1 + (1+x)^2 - (1+x)^2 = 1

I’ll post this and take a look at your answer.

[Z-eng]

Saying method 1 and method was kinda misleading, a better way to talk about method 2 was to say that the solution was independent of the sides of the 2 squares so regardless of their sizes, as long as the smaller square's side length is >= 1, the area of the red part is gonna be 1.
Then take a case with the alignment you did in method 2 to show that the argument still holds up

[KipIngram]

We're not told the length of the segment to the right of the length=1 segment, so it must be the case that the answer is independent of that value. So we can choose it to simplify our work. I choose for the length=1 segment to be the entire bottom of the square (i.e., the length to the right is zero). So the "straight" square is a unit square, and the tipped square thus has side length sqrt(2). The diagonal of the unit square is also sqrt(2), and so the top-right corner of the unit square is in the center of the tipped square. The red area is thus half the area of the tipped square. The tipped square has side length sqrt(2), so its area is 2. Therefore,

Red Area = 1

Q.E.D.

PS: If we had been given an explicit case - a value for the length of the segment to the right of the unit segment, then we'd have had to do a lot more work. We wouldn't have gotten to invoke the independent of the result on that value. This sort of thing is always worth looking out for in "test environment" problems that are not entirely specified.

[johngutwirth]

THX for the nice problem and solutions. The purpose of a nagging musical background is beyond me though!