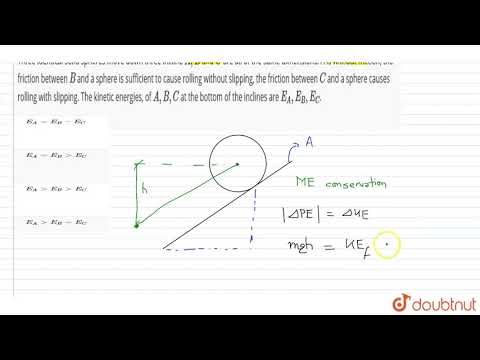
Three identical solid spheres move down three incline \( A, B \) and \( C \) are all of the same...

Three identical solid spheres move down three incline \( A, B \) and \( C \) are all of the same dimensions. \( A \) is without friction,
\( \mathrm{P} \) the friction between \( B \) and a sphere is sufficient to cause

W rolling without slipping, the friction between \( C \) and a sphere causes rolling with slipping. The kinetic energies of \( A, B, C \) at the bottom of the inclines are \( E_{A}, E_{B}, E_{C} \) :
(1) \( E_{A}=E_{B}=E_{C} \)
(2) \( E_{A}=E_{B}E_{C} \)
(3) \( E_{A}E_{B}E_{C} \)
(4) \( E_{A}E_{B}=E_{C} \)