Lecture 27: Minimum Spanning Trees, Cut Property, Kruskal's Algorithm [Advanced Data Structures]

In this lecture, I discuss what a minimum spanning tree is, optimization problems, the cut property of minimum spanning trees (and its proof), and Kruskal's algorithm. Next time we will talk about Prim's Algorithm.

About Kruskal's Algorithm: Note that when you implement Kruskal's Algorithm, normally you sort the edges by their weights (smallest to largest), then you scan from left to right finding the least-weight edge that connects two clusters. Hence, the need for the union-find disjoint set data structure. I state this during the lecture.

Remark: I think I'm a bit clearer in the notes on what the "clusters" are, as disjoint sets.

Want the notes, and/or want to support my mission? Look no further, get the written companion to this video lectures series. Buy the book, Advanced Data Structures: An Introduction to Data Structures and Algorithms, it is available at the below links (by format, given in parentheses):

Supporters (to date of publication, by tier (top to bottom)):
----------------------------------------------------------
Patreon Supporters (General Support):
-Draikou
Patreon Supporters (Basic Support):
-Eric R
-Tor Asbjørn Bekkelund
Patreon Supporters (Special Thank You, and Supporter Access!):
-TracyMae
-----------------------------------------------------------
Become a supporter today! To support my work and mission to provide free or accessible Computer Science education (especially in theory), subscribe to the channel, share my videos. Please donate and contribute to support my work for more content:

Follow also at:

Time Stamps:
0:00 What is a weighted graph?
4:02 Why consider weighted graphs?
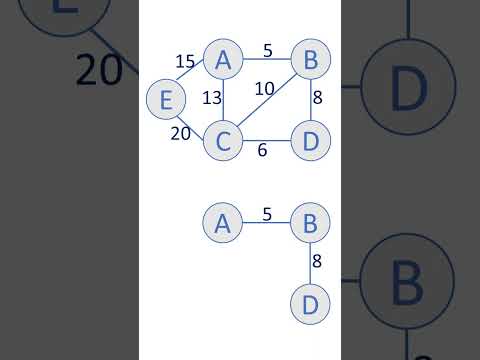
6:40 What is a minimum spanning tree (MST)?
9:25 Example of a MST.
11:10 MST Problem, what is an optimization problem?
14:35 Applications of MSTs
20:20 Cut Property of MSTs
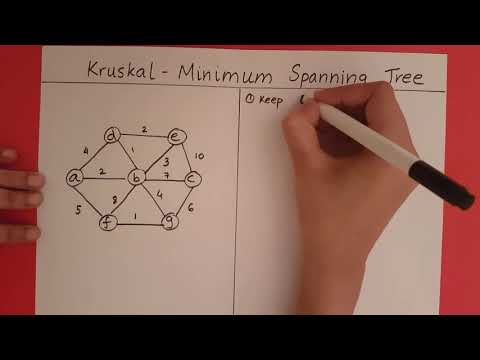
35:30 Kruskal's Algorithm

Have a beautiful day!

#Graphs
#ComputerScience
#DataStructures