filmov
tv
If ax²+2hxy+by²+2gx+2fy+c=0 RepresntsAPairOfParallelLinesThenShowThatDistanceBetween2ParallelLines

Показать описание
Junior Inter Maths1B #PairOfStraightLines LAQ 7 Marks VIP Questions With Complete Solutions
If ax^2+2hxy+by^2 = 0 Represents a pair of straight lines Then Cosβ = | a + b | / √[(a - b)^2 + 4h^2]
Show that the product of the perpendicular distance from a point (α, β) to the pair of straight lines represented by ax^2 + 2hxy + by^2 = 0 is | aα^2 + 2hαβ + bβ^2 | by √[(a - b)^2 + 4h^2]
Starts from 13:30 Seconds in the same video & link
Show that the Product Of Perpendicular Distances From the point Origin To the pair of straight lines represented by ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0 is | c | / √[(a - b)^2 + 4h^2]
Show that Area of Δ formed by the pair of lines ax^2 + 2hxy + by^2 = 0 & lx + my + n = 0 is |[n^2√(h^2 - ab)]/(am^2 - 2hlm + bl^2)|
If ax^2+2hxy+by^2+2gx+2fy+c=0 Represnts A Pair Of Parallel Lines Then Show That h^2 = ab, af^2 = bg^2, The Distance between 2 Parallel Lines = 2√[g^2 - ac]/(a[a + b]) = 2√[f^2 - bc]/(b[a + b])
If ax^2 + 2hxy + by^2 = 0 represents a pair of lines then show that equation of pair of Angular Bisectors is h(x^2 - y^2) = (a - b)xy
Find the values of k, if the lines joining the origin to the point of intersection of the curve 2x^2 – 2xy + 3y^2 + 2x – y – 1 = 0 and the line x + 2y = k are mutually perpendicular.
Show that the lines joining the origin to the points of intersection of the curve x^2 – xy + y^2 + 3x + 3y – 2 = 0 and the straight line x - y - √2 = 0 are mutually perpendicular
Show That The Lines Joining The Origin To The Points Of Intersection Of The Curve 7x^2-4xy+8y^2+2x-4y-8=0 & The Line 3x-y=2 are mutually perpendicular
Find The Condition For The Chord lx+my=1 Of The Circle x^2+y^2=a^2 whose centre is the origin To Subtend A Right Angle At The Origin
Find the condition for the lines joining the origin to the points of intersection of the circle x^2 + y^2 = a^2 and the line l x + m y = 1 to coincide
Find the angle between the lines joining the origin to the point of intersection of the curve x^2 + 2xy + y^2 + 2x + 2y - 5 = 0 and the line 3x - y + 1 = 0
Find the Lines Joining Origin To Point Of Intersection Of the curve 7x^2-4xy+8y^2+2x-4y-8=0 with the line 3x-y=2. Also find the angle between them
#MathsShorts
#Shorts
#YouTubeShorts
#SuperShorts
#AmazingShorts
#1MinuteBrainTeaser
#AbacusMathsTricks
#AmazingMathsTricks
#FastMathsTricks
#FastBrainTest
#FunMaths
#MathsPuzzle
#MathsRiddles
#MathsMental
#MentalMaths
#MindBooster
#MindBlowingMathsTricks
#QuickIQTest
#Shorts
#SimpleMathsRiddles
#SimpleMaths
#SpeedMaths
#TimePassMaths
#TrendingMaths
#VedhaGanithamTricks
#VedicMathsTricks
#ViralMaths
#WhatsapStatus
#YouTubeShorts
#YTShorts
If ax^2+2hxy+by^2 = 0 Represents a pair of straight lines Then Cosβ = | a + b | / √[(a - b)^2 + 4h^2]
Show that the product of the perpendicular distance from a point (α, β) to the pair of straight lines represented by ax^2 + 2hxy + by^2 = 0 is | aα^2 + 2hαβ + bβ^2 | by √[(a - b)^2 + 4h^2]
Starts from 13:30 Seconds in the same video & link
Show that the Product Of Perpendicular Distances From the point Origin To the pair of straight lines represented by ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0 is | c | / √[(a - b)^2 + 4h^2]
Show that Area of Δ formed by the pair of lines ax^2 + 2hxy + by^2 = 0 & lx + my + n = 0 is |[n^2√(h^2 - ab)]/(am^2 - 2hlm + bl^2)|
If ax^2+2hxy+by^2+2gx+2fy+c=0 Represnts A Pair Of Parallel Lines Then Show That h^2 = ab, af^2 = bg^2, The Distance between 2 Parallel Lines = 2√[g^2 - ac]/(a[a + b]) = 2√[f^2 - bc]/(b[a + b])
If ax^2 + 2hxy + by^2 = 0 represents a pair of lines then show that equation of pair of Angular Bisectors is h(x^2 - y^2) = (a - b)xy
Find the values of k, if the lines joining the origin to the point of intersection of the curve 2x^2 – 2xy + 3y^2 + 2x – y – 1 = 0 and the line x + 2y = k are mutually perpendicular.
Show that the lines joining the origin to the points of intersection of the curve x^2 – xy + y^2 + 3x + 3y – 2 = 0 and the straight line x - y - √2 = 0 are mutually perpendicular
Show That The Lines Joining The Origin To The Points Of Intersection Of The Curve 7x^2-4xy+8y^2+2x-4y-8=0 & The Line 3x-y=2 are mutually perpendicular
Find The Condition For The Chord lx+my=1 Of The Circle x^2+y^2=a^2 whose centre is the origin To Subtend A Right Angle At The Origin
Find the condition for the lines joining the origin to the points of intersection of the circle x^2 + y^2 = a^2 and the line l x + m y = 1 to coincide
Find the angle between the lines joining the origin to the point of intersection of the curve x^2 + 2xy + y^2 + 2x + 2y - 5 = 0 and the line 3x - y + 1 = 0
Find the Lines Joining Origin To Point Of Intersection Of the curve 7x^2-4xy+8y^2+2x-4y-8=0 with the line 3x-y=2. Also find the angle between them
#MathsShorts
#Shorts
#YouTubeShorts
#SuperShorts
#AmazingShorts
#1MinuteBrainTeaser
#AbacusMathsTricks
#AmazingMathsTricks
#FastMathsTricks
#FastBrainTest
#FunMaths
#MathsPuzzle
#MathsRiddles
#MathsMental
#MentalMaths
#MindBooster
#MindBlowingMathsTricks
#QuickIQTest
#Shorts
#SimpleMathsRiddles
#SimpleMaths
#SpeedMaths
#TimePassMaths
#TrendingMaths
#VedhaGanithamTricks
#VedicMathsTricks
#ViralMaths
#WhatsapStatus
#YouTubeShorts
#YTShorts
Комментарии
 0:11:29
0:11:29
 0:30:26
0:30:26
 0:02:10
0:02:10
 0:02:19
0:02:19
 0:15:16
0:15:16
 0:02:25
0:02:25
 0:09:09
0:09:09
 0:06:49
0:06:49
 0:21:01
0:21:01
 0:32:00
0:32:00
 0:03:07
0:03:07
 0:07:18
0:07:18
 0:10:27
0:10:27
 0:16:00
0:16:00
 0:06:52
0:06:52
 0:08:35
0:08:35
 0:05:41
0:05:41
 0:12:47
0:12:47
 0:00:12
0:00:12
 0:08:01
0:08:01
 0:40:39
0:40:39
 0:17:03
0:17:03
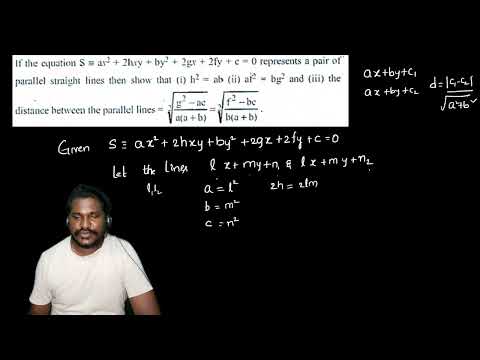 0:09:56
0:09:56
 0:01:00
0:01:00