filmov
tv
Time Complexity analysis of recursion - Fibonacci Sequence
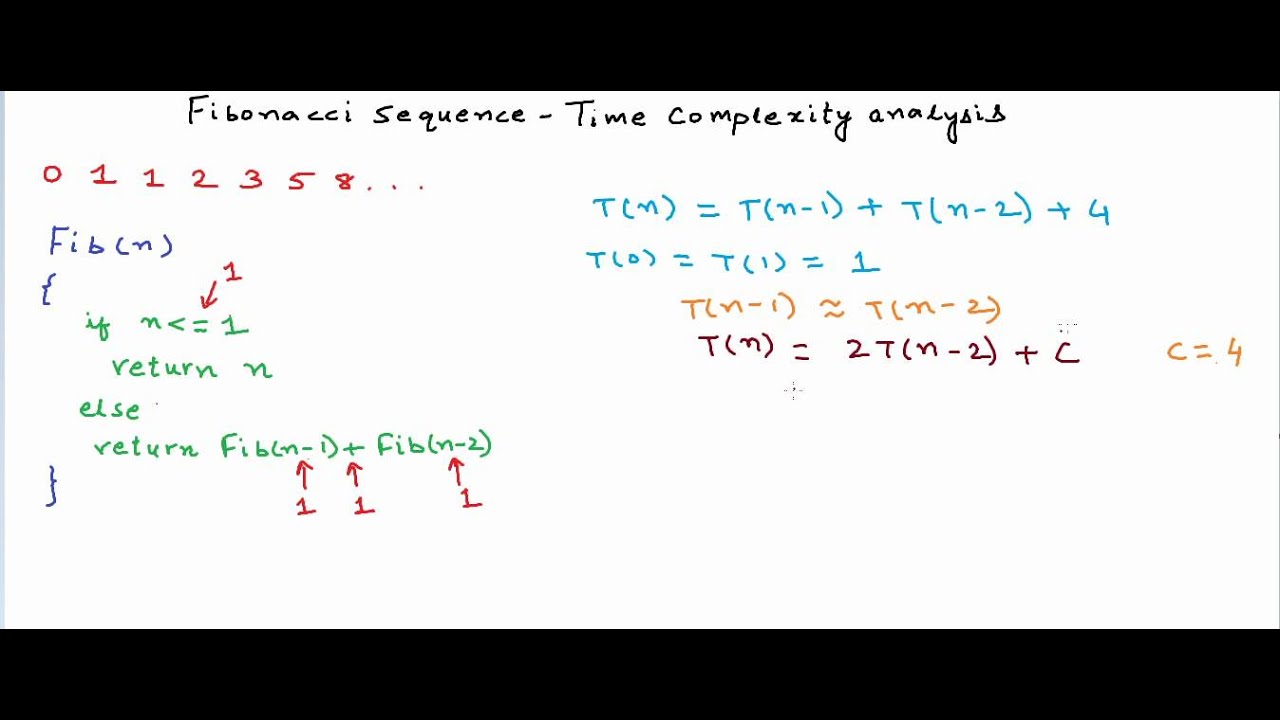
Показать описание
See complete series on recursion here
In this lesson, we will analyze time complexity of a recursive implementation of Fibonacci sequence.
Prerequisite: basic knowledge of recursion as programming concept, basic understanding time complexity analysis.
In this lesson, we will analyze time complexity of a recursive implementation of Fibonacci sequence.
Prerequisite: basic knowledge of recursion as programming concept, basic understanding time complexity analysis.
Understanding Time complexity of recursive functions
Time Complexity analysis of recursion - Fibonacci Sequence
Time and space complexity analysis of recursive programs - using factorial
Exponentiation - Time Complexity analysis of recursion
Finding runtime complexity of recursive algorithm
Fibonacci: Time Complexity | Solved Problems | GateAppliedcourse
2.1.1 Recurrence Relation (T(n)= T(n-1) + 1) #1
Fibonacci Sequence - Anatomy of recursion and space complexity analysis
21. Merge Intervals | Arrays - Hard | Learn DSA | Leetcode 56
Time and Space Complexity analysis of recursive programs | InterviewBit
Calculating Time Complexity | Data Structures and Algorithms| GeeksforGeeks
Asymptotic Analysis (Solved Problem 1)
Introduction to Big O Notation and Time Complexity (Data Structures & Algorithms #7)
Analysis of Recursive Algorithms
1.5.1 Time Complexity #1
Analysis of Recursion 1 - Factorial and the Substitution Method
L-2.9: Recurrence Relation [T(n)= 2T(n/2) +cn] | Recursive Tree method | Algorithm
Module 1 Time Complexity Analysis of Recursive Algorithms
M269 - CH6 -Time Complexity analysis of recursion - Fibonacci Sequence (ch6)
7 Time Complexity of a Recursive Tree
Factorial: Time and Space complexity | Recursion in programming| DS & Algorithm | Gate Appliedco...
Time Complexity of the Euclid's Recursive GCD Algorithm
L-2.3: Recurrence Relation [ T(n)= n*T(n-1) ] | Substitution Method | Algorithm
Exponentiation - Time Complexity Analysis Of Recursion - Coding With Mr. Ash
Комментарии
 0:05:35
0:05:35
 0:09:28
0:09:28
 0:08:03
0:08:03
 0:08:28
0:08:28
 0:02:38
0:02:38
 0:07:03
0:07:03
 0:13:48
0:13:48
 0:09:39
0:09:39
 0:11:38
0:11:38
 0:05:42
0:05:42
 0:08:05
0:08:05
 0:07:23
0:07:23
 0:36:22
0:36:22
 0:27:20
0:27:20
 0:10:08
0:10:08
 0:18:04
0:18:04
 0:07:14
0:07:14
 0:18:59
0:18:59
 0:26:55
0:26:55
 0:25:43
0:25:43
 0:21:14
0:21:14
 0:07:52
0:07:52
 0:07:40
0:07:40
 0:08:28
0:08:28