filmov
tv
Inverse Secant (ArcSecant) | How to Find the Exact Value | (MathAngel369)

Показать описание
Inverse Secant | How to Find the Exact Value
🖤Subscribe to this channel:
In this video, we are going to learn how to evaluate inverse secant.
Key things to consider:
🔹Observing the domain
🔹Converting sec(y) to cos(y)
🔹Observing the Unit Circle
🔹Observing the Range
🔹Choosing the Value
◻️◻️◻️Concepts◻️◻️◻️
When working with inverse trig functions, in particularly, inverse secant, you will have an equation in the form
y = sec^-1(x)
🔷Domain:
Note that the domain of sec^-1(x) is the set of all x such that sec^-1(x) is defined.
In other words, you can think of the domain as all your possible “input” values.
sec^-1(x) defined is defined on the interval
(-inf, -1] U [1, inf)
Thus, we say that the domain of sec^-1(x) is
(-inf, -1] U [1, inf)
Next, we check to see if the x-value satisfies the domain.
If the x-value does not satisfy the domain, we simply say that there is no solution.
If the x-value is within the domain, we then take the secant of both sides to get
sec(y) =x.
🔷Converting sec(y) to cos(y):
Now it is much easier to evaluate cos(y) instead of
sec(y).
Thus, we use the fact that
sec(y) =1/cos(y) or cos(y) =1/sec(y)
Hence, sec(y) =x can be rewritten as
cos(y) = 1/x
🔷Observing the Unit Circle:
Looking at the unit circle, you will see terminal points in the form, (a,b).
Remember that cos(y) takes the “a” coordinate of the terminal point.
We then search for all the values of y such that
cos(y) = 1/x
where 1/x is in the “a” location of (a,b).
Once we find all the values for y, we consider the range of sec^-1(x).
🔷Observing the Range:
While the domain is your possible input values, the range your possible output values.
The range of sec^-1(x) is
[0,pi/2)U(pi/2,pi],
which is the upper region of the unit circle, but not including pi/2.
🔷Choosing the Value
Sometimes, you may find multiple values for y; however, we must choose the value for y that satisfies the range.
◻️◻️◻️Example◻️◻️◻️
Let’s say we have
y = sec^-1(-2).
Here are the steps:
🔷Observing the Domain
Note that the domain of sec^-1(x) is
(-inf,-1] U [1,inf)
Since x is equal to -2 in our example, we know that it satisfies the domain.
Since our x-value is within the domain of sec^-1(x), we then take the secant of both sides to get
sec(y) = -2.
🔷Converting sec(y) to cos(y):
Again, it is much easier to evaluate cos(y) instead of sec(y).
So we use the fact that
sec(y) =1/cos(y) or cos(y) =1/sec(y)
Thus, sec(y) = -2 can be rewritten as
cos(y) = -1/2.
🔷Observing the Unit Circle
Looking at the unit circle, we search for all the values of y such that cos(y) = -1/2. Or sometimes I like to ask myself, “Where on the unit circle does cos(y)= -1/2?”
On the unit circle, we have terminal points
(a,b) = (-1/2, sqrt(3)/2) at the following angles:
2pi/3 (If we go in the positive direction)
-4pi/3 (If we go in the negative direction)
and we have terminal points
(a,b) = (-1/2, -sqrt(3)/2) at the following angles:
4pi/3 (If we go in the positive direction)
-2pi/3 (If we go in the negative direction)
Remember, we observe the “a” coordinate when working with cosine.
Thus, when:
y= 2pi/3, -4pi/3, 4pi/3, -2pi/3
we get:
cos(2pi/3)=-1/2
cos(-4pi/3)=-1/2
cos(4pi/3)=-1/2
cos(-2pi/3)=-1/2
🔷Observing the Range:
Now, we cannot choose any value for y in our ultimate answer. We must consider the range of sec^-1(x).
The range of sec^-1(x) is
[0,pi/2)U(pi/2,pi]
which is the upper region of the unit circle, but not including pi/2.
🔷Choosing the Value
Remember that we must be sure that our value for y is within the range!
We see that the only value within the range is
2pi/3.
Thus, we choose 2pi/3.
Hence,
cos(2pi/3) =-1/2,
which means that
sec(2pi/3)=-2,
which means that
2pi/3= sec^-1(-2),
and we say that
y=2pi/3
We are done!
Thank you for watching! If you have any questions, if this video helps, or if you would like to provide any feedback, let me know in the comments!
***
Need more examples?
Here are suggested videos from this channel:
🎥 Inverse Sine | How to Find the Exact Value
🎥 Inverse Cosine | How to Find the Exact Value
🎥 Inverse Tangent | How to Find the Exact Value
🎥 Inverse Cotangent | How to Find the Exact Value
🎥 Inverse Cosecant | How to Find the Exact Value
************
📝Here is my Blog Post Associated with This Video:
****
Find Me on Social Media!
➕ MathAngel369➕
▪️YouTube
▪️Instagram:
▪️Facebook:
▪️Website:
▪️Blog
*****************
#MathAngel369 #InverseTrigFunctions
🖤Subscribe to this channel:
In this video, we are going to learn how to evaluate inverse secant.
Key things to consider:
🔹Observing the domain
🔹Converting sec(y) to cos(y)
🔹Observing the Unit Circle
🔹Observing the Range
🔹Choosing the Value
◻️◻️◻️Concepts◻️◻️◻️
When working with inverse trig functions, in particularly, inverse secant, you will have an equation in the form
y = sec^-1(x)
🔷Domain:
Note that the domain of sec^-1(x) is the set of all x such that sec^-1(x) is defined.
In other words, you can think of the domain as all your possible “input” values.
sec^-1(x) defined is defined on the interval
(-inf, -1] U [1, inf)
Thus, we say that the domain of sec^-1(x) is
(-inf, -1] U [1, inf)
Next, we check to see if the x-value satisfies the domain.
If the x-value does not satisfy the domain, we simply say that there is no solution.
If the x-value is within the domain, we then take the secant of both sides to get
sec(y) =x.
🔷Converting sec(y) to cos(y):
Now it is much easier to evaluate cos(y) instead of
sec(y).
Thus, we use the fact that
sec(y) =1/cos(y) or cos(y) =1/sec(y)
Hence, sec(y) =x can be rewritten as
cos(y) = 1/x
🔷Observing the Unit Circle:
Looking at the unit circle, you will see terminal points in the form, (a,b).
Remember that cos(y) takes the “a” coordinate of the terminal point.
We then search for all the values of y such that
cos(y) = 1/x
where 1/x is in the “a” location of (a,b).
Once we find all the values for y, we consider the range of sec^-1(x).
🔷Observing the Range:
While the domain is your possible input values, the range your possible output values.
The range of sec^-1(x) is
[0,pi/2)U(pi/2,pi],
which is the upper region of the unit circle, but not including pi/2.
🔷Choosing the Value
Sometimes, you may find multiple values for y; however, we must choose the value for y that satisfies the range.
◻️◻️◻️Example◻️◻️◻️
Let’s say we have
y = sec^-1(-2).
Here are the steps:
🔷Observing the Domain
Note that the domain of sec^-1(x) is
(-inf,-1] U [1,inf)
Since x is equal to -2 in our example, we know that it satisfies the domain.
Since our x-value is within the domain of sec^-1(x), we then take the secant of both sides to get
sec(y) = -2.
🔷Converting sec(y) to cos(y):
Again, it is much easier to evaluate cos(y) instead of sec(y).
So we use the fact that
sec(y) =1/cos(y) or cos(y) =1/sec(y)
Thus, sec(y) = -2 can be rewritten as
cos(y) = -1/2.
🔷Observing the Unit Circle
Looking at the unit circle, we search for all the values of y such that cos(y) = -1/2. Or sometimes I like to ask myself, “Where on the unit circle does cos(y)= -1/2?”
On the unit circle, we have terminal points
(a,b) = (-1/2, sqrt(3)/2) at the following angles:
2pi/3 (If we go in the positive direction)
-4pi/3 (If we go in the negative direction)
and we have terminal points
(a,b) = (-1/2, -sqrt(3)/2) at the following angles:
4pi/3 (If we go in the positive direction)
-2pi/3 (If we go in the negative direction)
Remember, we observe the “a” coordinate when working with cosine.
Thus, when:
y= 2pi/3, -4pi/3, 4pi/3, -2pi/3
we get:
cos(2pi/3)=-1/2
cos(-4pi/3)=-1/2
cos(4pi/3)=-1/2
cos(-2pi/3)=-1/2
🔷Observing the Range:
Now, we cannot choose any value for y in our ultimate answer. We must consider the range of sec^-1(x).
The range of sec^-1(x) is
[0,pi/2)U(pi/2,pi]
which is the upper region of the unit circle, but not including pi/2.
🔷Choosing the Value
Remember that we must be sure that our value for y is within the range!
We see that the only value within the range is
2pi/3.
Thus, we choose 2pi/3.
Hence,
cos(2pi/3) =-1/2,
which means that
sec(2pi/3)=-2,
which means that
2pi/3= sec^-1(-2),
and we say that
y=2pi/3
We are done!
Thank you for watching! If you have any questions, if this video helps, or if you would like to provide any feedback, let me know in the comments!
***
Need more examples?
Here are suggested videos from this channel:
🎥 Inverse Sine | How to Find the Exact Value
🎥 Inverse Cosine | How to Find the Exact Value
🎥 Inverse Tangent | How to Find the Exact Value
🎥 Inverse Cotangent | How to Find the Exact Value
🎥 Inverse Cosecant | How to Find the Exact Value
************
📝Here is my Blog Post Associated with This Video:
****
Find Me on Social Media!
➕ MathAngel369➕
▪️YouTube
▪️Instagram:
▪️Facebook:
▪️Website:
▪️Blog
*****************
#MathAngel369 #InverseTrigFunctions
 0:05:05
0:05:05
 0:02:09
0:02:09
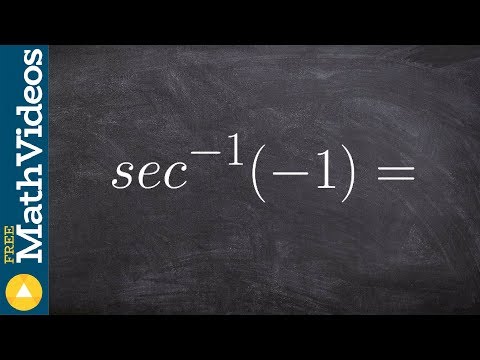 0:02:49
0:02:49
 0:00:40
0:00:40
 0:04:42
0:04:42
 0:00:57
0:00:57
 0:10:19
0:10:19
 0:17:31
0:17:31
 0:06:43
0:06:43
 0:05:46
0:05:46
 0:04:03
0:04:03
 0:07:52
0:07:52
 0:12:46
0:12:46
 0:00:59
0:00:59
 0:17:13
0:17:13
 0:02:19
0:02:19
 0:12:14
0:12:14
 0:06:33
0:06:33
 0:01:30
0:01:30
 0:04:44
0:04:44
 0:09:14
0:09:14
 0:04:58
0:04:58
 0:10:30
0:10:30
 0:13:38
0:13:38