Given a semicircle and a green circle inside a quarter circle, find the area of the green circle.

preview_player
Показать описание
Find the area of the green circle by drawing triangles and using the Pythagorean Theorem.
  1. The Math District
  2. geometry
  3. triangle
  4. right triangle
  5. Pythagorean theorem
  6. quarter circle
Рекомендации по теме
Given a semicircle 0:09:52

Given a semicircle and a green circle inside a quarter circle, find the area of the green circle.

If Given a 0:06:47

If Given a Semicircle with a Right Triangle, Find the Value of the Line Segment X | Easy Tutorial

Graphing a Semicircle 0:04:09

Graphing a Semicircle given an Algebraic Expression

How To Calculate 0:05:07

How To Calculate The Area of a Semicircle

Can You Calculate 0:04:38

Can You Calculate the RADIUS of the Semicircle in the Given Figure? | Minute Math

Find the blue 0:08:09

Find the blue area | Geometry problem | Given a semicircle and a quarter circle inside a rectangle

How To Calculate 0:05:35

How To Calculate The Perimeter of a Semicircle

Find the blue 0:13:24

Find the blue shaded area | Given a semicircle inside a quarter circle | Geometry Problem | 2 Method

Give formula for 0:02:31

Give formula for area in terms of x. A semicircle of diameter x, a semicircular of radius x

Two circles and 0:24:35

Two circles and a semicircle with a given radius is inscribed in a circle.

Find the blue 0:06:02

Find the blue shaded area | Given a semicircle and a quarter circle inside a rectangle | Geometry

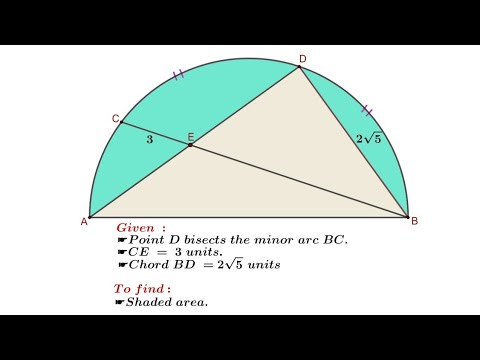
Shaded area = 0:10:16

Shaded area = ?? In the given semicircle, CE = 3 units and BD = 2√5 units. Arc BD = Arc DC.

Geometry: Given areas 0:08:57

Geometry: Given areas of triangles within a semi-circle, find the radius | CAT, High School Geometry

Find AB, given 0:04:58

Find AB, given a triangle inscribed in a semicircle.

Unveiling the Area 0:03:11

Unveiling the Area of a Semicircle with Given Chord Length

371.In given fig 0:01:55

371.In given fig ADC is a semi circle,BD perpendicular to AC,AB=8,BC=2 then find BD (Code-371)

Can You Find 0:04:27

Can You Find the Area of Given Semi-circle in 30 seconds | Tricky Geometry Problem

Find the radius 0:00:27

Find the radius of given semi circle inside the right angle triangle #mathematics #technology

In the given 0:04:22

In the given figure, AB is the diameter of the largest semi-circle. AB= 21 cm, AM=MN=NB ...

radius and diameter 0:06:29

radius and diameter of a semicircle when area is given

Find the Area 0:06:48

Find the Area of Semi-circle Given Two Inscribed Triangles

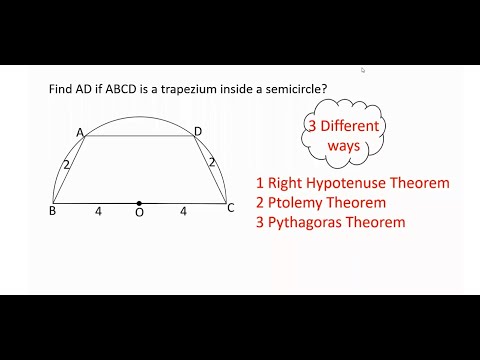
A trapezium is 0:07:58

A trapezium is given inside a semicircle with 3 sides given

Mechanical Engineering: Centroids 0:04:29

Mechanical Engineering: Centroids & Center of Gravity (6 of 35) Center of Gravity of a Semi Circ...

Solving perimeter of 0:01:46

Solving perimeter of a semi circle when radius is given

Комментарии
Автор

تمرين جميل جيد . رسم واضح مرتب . شرح واضح مرتب. شكرا جزيلا لكم والله يحفظكم ويرعاكم ويحميكم . تحياتنا لكم من غزة فلسطين .

اممدنحمظ
Автор

Can it be assumed, or better yet proven, that triangle ABO is is an isosceles triangle ? If that is the case then 8+x = 16-x and we can skip all of the fancy algebra. You just demonstrated that in this particular case it is.

larrydickenson
Автор

what if you would place a third circle that is tangent to green circle, diameter of the quarter circle and the edge of the quarter circle. What would the radius be of that smaller circle?

tgrgt
Автор

Seems you could go faster, assuming that ABO is an isocele triangle, AB=OB, so 8+x=16-x and you find that x=4. But how can you prove it first?

MrMichelX
Автор

Green circle radius = r/4 = 16/4 = 4
Then it's Area = πr² = 16π
Add on :- Pink circle radius = r/2 = 16/2= 8

amitanand
Автор

It looks better to stop at BE^2 and avoid estimating BE and than squaring it twice, i.e. final equation should be BE^2(AEB)=BE^2(OEB).
Thumb up any case.

michaelkouzmin