filmov
tv
Abstract Algebra, Lec 2B: Equivalence Relations, Partitions, Induction, Foundational Number Theory

Показать описание
(0:00) Equivalence Relations and Partitions.
(9:57) Story about Gauss adding up the first 100 integers in his head.
(13:03) Use (the first principle of) mathematical induction to prove that the sum of the first n integers is n(n+1)/2.
(23:15) Mention well-ordering principle is an axiom.
(23:25) Number theory: division algorithm, dividend, divisor, quotient, remainder, divides, factor, multiple, prime, composite, fundamental theorem of arithmetic, greatest common divisor (gcd), gcd is a linear combination, gcd in terms of prime factorization, relatively prime (coprime) integers.
Bill Kinney, Bethel University mathematics department
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Abstract Algebra, Lec 2B: Equivalence Relations, Partitions, Induction, Foundational Number Theory
(Abstract Algebra 1) Partitions and Equivalence Relations
BEST DEFENCE ACADEMY IN DEHRADUN | NDA FOUNDATION COURSE AFTER 10TH | NDA COACHING #shorts #nda #ssb
🔥 POV: Integration - Look at me! 👀 💪 | JEE 2024 | Math | Bhoomika Ma'am
Jaldi Wahan Se Hato! IIT Delhi version! #iit #iitjee #iitdelhi
Functions IIT Questions NO 11 ( X Class)
Comment yes for more body language videos! #selfhelp #personaldevelopment #selfimprovement
Logical Reasoning???#viral #vidumzn
1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet
Abstract Algebra Lecture 3 : Equivalence Relations
Pakistan education system what a beautiful environment WOW🤣🤣
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
Sets and Functions -- Abstract Algebra 1
Aspirants practicing eatingetiquette # SSB #SSBPreparation #NDA #CDS #Defence #DefenceAcademy
Cardinalities, abstract algebra -- Proofs
Abstract Alg, Lec 2A: Group Examples, Modular Arithmetic, Sets & Functions, Composition of Funct...
Abstract Algebra 1
Abstract Algebra II: basic module theory, 3-18-22 part 1
Tamasha Dekho 😂 IITian Rocks Relatives Shock 😂😂😂 #JEEShorts #JEE #Shorts
Ducky first meeting with his wife aroob jatoi#makhan
Equivalence Relations & Set Partitions, Part One
Lecture 6: Equivalence relations
Construct Fields of Order 5^2 = 25 and 3^3 = 27 (Prime Power Order) as Factor Rings of ℤp[x]
Equivalence Relations and Partitions(lec#6)
Комментарии
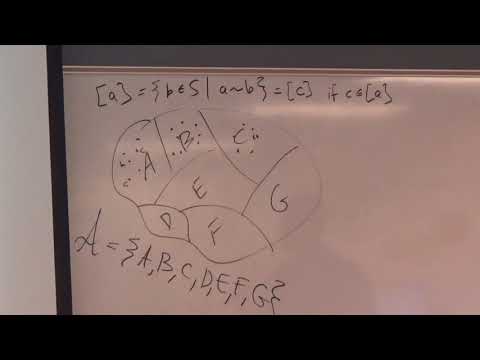 0:32:04
0:32:04
 0:06:35
0:06:35
 0:00:15
0:00:15
 0:00:48
0:00:48
 0:00:17
0:00:17
 0:00:48
0:00:48
 0:00:22
0:00:22
 0:00:11
0:00:11
 0:00:20
0:00:20
 0:37:34
0:37:34
 0:00:16
0:00:16
 0:00:12
0:00:12
 0:28:53
0:28:53
 0:00:11
0:00:11
 0:48:04
0:48:04
 0:34:28
0:34:28
 1:29:01
1:29:01
 0:59:51
0:59:51
 0:00:13
0:00:13
 0:00:20
0:00:20
 0:09:13
0:09:13
 0:38:48
0:38:48
 0:20:32
0:20:32
 0:17:10
0:17:10