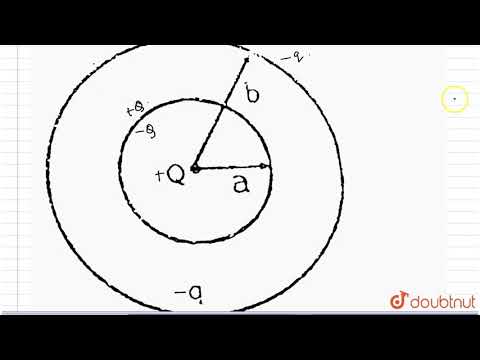
In the figure, the inner (shaded) region \( A \) represents a sphere of radius \( r_{A}=1 \), wi...

In the figure, the inner (shaded) region \( A \) represents a sphere of radius \( r_{A}=1 \), within which the electrostatic charge density varies with the radial distance \( r \) from the center as \( \rho_{A}=k r \), where \( k \) is positive. In the spherical shell \( B \) of outer radius \( r_{B} \), the electrostatic charge density varies as \( \rho_{B}=\frac{2 k}{r} \). Assume that dimensions are taken care of. All physical quantities are in their SI units.
Which of the following statement(s) is(are) correct?
(a) If \( r_{B}=\sqrt{\frac{3}{2}} \), then the electric field is zero everywhere outside \( B \)
(b) If \( r_{B}=\frac{3}{2} \), then the electric potential just outside \( B \) is \( \frac{k}{\epsilon} \)
(c) If \( r_{B}=2 \), then the total charge of the configuration is \( 15 \pi k \)
(d) If \( r_{B}=\frac{5}{2} \), then the magnitude of the electric field just outside \( B \) is \( \frac{13 \pi k}{\epsilon_{0}} \)