sup (a+S)=a+sup(S) | Properties of Supremum and Infimum | Real Analysis

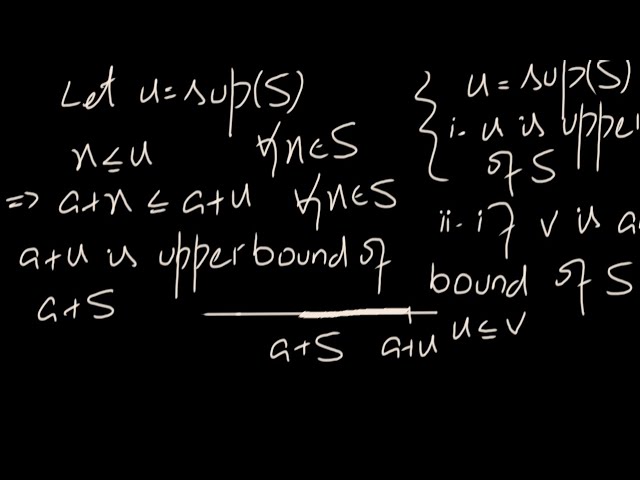
preview_player
Показать описание
In this class we will discuss about Prove of
sup (a+S)=a+sup(S)
and
inf (a+S)=a+inf(S)
  1. Mathnasium Plus
  2. Mathnasium
  3. Plus
  4. sup (a S)=a sup(S)
  5. supremum
  6. upper bound
Рекомендации по теме
sup (a+S)=a+sup(S) | 0:11:52

sup (a+S)=a+sup(S) | Properties of Supremum and Infimum | Real Analysis

Sup(S+T) = Sup 0:13:29

Sup(S+T) = Sup S + Sup T |proof| |property of supremum |BSc3rdyr|UPSC optional|L30

Proof! sup(aS)=a(sup S) 0:05:48

Proof! sup(aS)=a(sup S) (Real Analysis)

36 Sup of 0:08:37

36 Sup of set cS when c is positive

inf(S) = -sup(-S) 0:17:51

inf(S) = -sup(-S)

Sup(1- 1/n), n 0:04:28

Sup(1- 1/n), n is natural number | Sup(A) and Inf(A) | Use of Archimedean Property

Fundamental Properties of 0:15:46

Fundamental Properties of Supremum and Infimum, Including sup(A + B) = sup(A) + sup(B)

Sup (A+B) = 0:17:05

Sup (A+B) = Sup A + Sup B | Properties of Supremum and Infimum | Real Analysis | Lease upper bound

Define supremum of 0:15:53

Define supremum of a set [sup(S)]

Supremum & Infimum: 0:09:15

Supremum & Infimum: Sup Of S(A+B) & Inf(A+B) I Jak Higher Mathematics

Supremum & Infimum: 0:04:24

Supremum & Infimum: α . sup S { inf(αs) if α less than 0 | Jak Higher Mathematics

Sup(a+S)=a+Sup(S)|Theorem of Supremum 0:24:35

Sup(a+S)=a+Sup(S)|Theorem of Supremum

Prove Sup(A) ≥ 0:03:19

Prove Sup(A) ≥ Inf(A)

2.5 Supremum: proof 0:03:21

2.5 Supremum: proof - sup(0,1)=1

38 Sup of 0:09:37

38 Sup of set S plus T

If a set 0:07:58

If a set S is closed and bounded then Sup S and Inf S belongs to the set S | Proof |

2nd condition (Case 0:04:00

2nd condition (Case 1) and (Case 2) α Inf S = Sup(αs) if α less than 0 I Jak Higher Mathematics

Properties of Sup 0:14:21

Properties of Sup and Inf (MTH320 L03-2)

PROLIMIT QUICK DRY 0:00:24

PROLIMIT QUICK DRY SUP JACKET

Amazing Discount on 0:00:16

Amazing Discount on our Windsurfing/SUP Instructor Course

Sup(A+B) = SupA 0:09:47

Sup(A+B) = SupA + SupB

sup(a.A)=a inf(A), inf(a.A)=a.sup(A), 0:26:52

sup(a.A)=a inf(A), inf(a.A)=a.sup(A), a is negative, Real Analysis I, Rudin, Bartle, Lec-17

sup(a+A)=a+sup(A), inf(a+A)=a+inf(A), Real 0:26:25

sup(a+A)=a+sup(A), inf(a+A)=a+inf(A), Real Analysis I, Rudin, Bartle, Lec-18

u = sup(S) 0:07:50

u = sup(S) iff for all v ∈ R, if v ﹤ u then there is some s ∈ S such that v ﹤ s, & u is upper bo...