Program 2 - Find minimum and Maximum Element in an Array | Competitive Programming in C++

Program 2 - Find minimum and Maximum Element in an Array | Competitive Programming in C++

Contact No - 9555031137

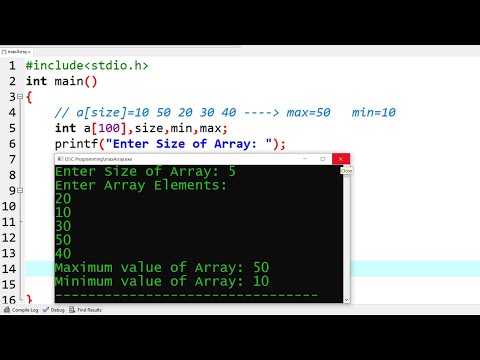
Given an array of size N. The task is to find the maximum and the minimum element of the array using the minimum number of comparisons.

Examples:

Input: arr[] = {3, 5, 4, 1, 9}
Output: Minimum element is: 1
Maximum element is: 9

Input: arr[] = {22, 14, 8, 17, 35, 3}
Output: Minimum element is: 3
Maximum element is: 35
First of all, how do we return multiple values from a function? We can do it either using structures or pointers.
We have created a structure named pair (which contains min and max) to return multiple values.
1. Maximum and minimum of an array using Sorting:
Approach:
One approach to find the maximum and minimum element in an array is to first sort the array in ascending order. Once the array is sorted, the first element of the array will be the minimum element and the last element of the array will be the maximum element.

Algorithm:

Initialize an array.
Sort the array in ascending order.
The first element of the array will be the minimum element.
The last element of the array will be the maximum element.
Print the minimum and maximum element.

Complexity Analysis:
The time complexity of this approach is O(n log n), where n is the number of elements in the array, as we are using a sorting algorithm. The space complexity is O(1), as we are not using any extra space.

Number of Comparisons:
The number of comparisons made to find the minimum and maximum elements is equal to the number of comparisons made during the sorting process. For any comparison-based sorting algorithm, the minimum number of comparisons required to sort an array of n elements is O(n log n). Hence, the number of comparisons made in this approach is also O(n log n).

2. Maximum and minimum of an array using Linear search:
Initialize values of min and max as minimum and maximum of the first two elements respectively. Starting from 3rd, compare each element with max and min, and change max and min accordingly (i.e., if the element is smaller than min then change min, else if the element is greater than max then change max, else ignore the element)

Time Complexity: O(n)
Auxiliary Space: O(1) as no extra space was needed.

In this method, the total number of comparisons is 1 + 2(n-2) in the worst case and 1 + n – 2 in the best case.
In the above implementation, the worst case occurs when elements are sorted in descending order and the best case occurs when elements are sorted in ascending order.

3. Maximum and minimum of an array using the tournament method:
Divide the array into two parts and compare the maximums and minimums of the two parts to get the maximum and the minimum of the whole array.

Time Complexity: O(n)
Auxiliary Space: O(log n) as the stack space will be filled for the maximum height of the tree formed during recursive calls same as a binary tree.

Total number of comparisons: let the number of comparisons be T(n). T(n) can be written as follows:
Algorithmic Paradigm: Divide and Conquer
4. Maximum and minimum of an array by comparing in pairs:
If n is odd then initialize min and max as the first element.
If n is even then initialize min and max as minimum and maximum of the first two elements respectively.
For the rest of the elements, pick them in pairs and compare their
maximum and minimum with max and min respectively.
Time Complexity: O(n)
Auxiliary Space: O(1) as no extra space was needed.