filmov
tv
Solve the equation sin x +cos x =1 | IB Math
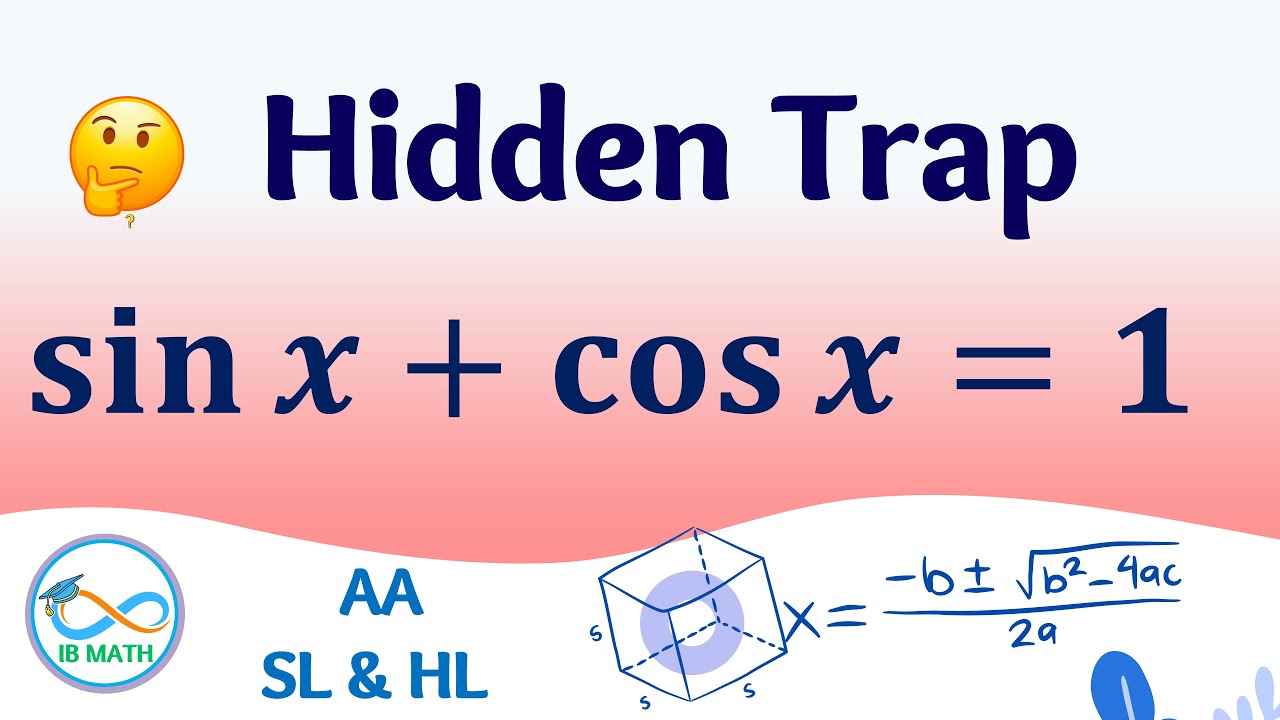
Показать описание
Welcome to IB Math Tutor Channel!
Are you an IB student struggling with Trigonometry ? This video is designed to help you master Trigonometry in the IB Mathematics curriculum, whether you're studying Analysis and Approaches (AA) or Applications and Interpretation (AI), at Standard Level (SL) or Higher Level (HL).
Understanding these concepts is crucial for your success in the IB Math exams. We break down complex ideas into simple, easy-to-follow steps to make your learning process smooth and effective.
IB Math Topics Covered:
Topic 3 Trigonometry
These topics form the foundation of the IB Math curriculum and are essential for achieving top grades.
Stay updated with our latest tutorials and tips:
Support Our Channel:
If you find this video helpful, please give it a thumbs up, share it with your friends, and leave a comment. Don't forget to hit the bell icon to get notified about our latest videos.
#IBMath #trigonometry #MathTutorial #Education #StudentSuccess #IBMathAA #IBMathAI #HighSchoolMath #MathHelp #ExamPreparation #StudyTips #Algebra #Functions #Trigonometry #Calculus #Statistics
Are you an IB student struggling with Trigonometry ? This video is designed to help you master Trigonometry in the IB Mathematics curriculum, whether you're studying Analysis and Approaches (AA) or Applications and Interpretation (AI), at Standard Level (SL) or Higher Level (HL).
Understanding these concepts is crucial for your success in the IB Math exams. We break down complex ideas into simple, easy-to-follow steps to make your learning process smooth and effective.
IB Math Topics Covered:
Topic 3 Trigonometry
These topics form the foundation of the IB Math curriculum and are essential for achieving top grades.
Stay updated with our latest tutorials and tips:
Support Our Channel:
If you find this video helpful, please give it a thumbs up, share it with your friends, and leave a comment. Don't forget to hit the bell icon to get notified about our latest videos.
#IBMath #trigonometry #MathTutorial #Education #StudentSuccess #IBMathAA #IBMathAI #HighSchoolMath #MathHelp #ExamPreparation #StudyTips #Algebra #Functions #Trigonometry #Calculus #Statistics
Комментарии
 0:03:13
0:03:13
 0:08:07
0:08:07
 0:03:42
0:03:42
 0:01:15
0:01:15
 0:06:47
0:06:47
 0:05:36
0:05:36
 0:00:48
0:00:48
 0:06:24
0:06:24
 0:29:29
0:29:29
 0:08:59
0:08:59
 0:04:59
0:04:59
 0:11:34
0:11:34
 0:06:48
0:06:48
 0:06:06
0:06:06
 0:02:06
0:02:06
 0:04:42
0:04:42
 0:04:04
0:04:04
 0:04:04
0:04:04
 0:04:30
0:04:30
![Solve sin(x+30)=2 cos(x+45),[0°,360°]](https://i.ytimg.com/vi/_VZ-_Me65l4/hqdefault.jpg) 0:07:20
0:07:20
 0:05:43
0:05:43
 0:05:35
0:05:35
 0:07:37
0:07:37
 0:00:49
0:00:49