filmov
tv
Mean and Variance of Poisson Distribution || Lesson 59 || Probability & Statistics | Learning Monkey

Показать описание
Mean and Variance of Poisson Distribution
In this class, We discuss Mean and Variance of Poisson Distribution.
The reader should have a prior knowledge og poisson distribution. Click Here.
Mean = µ = Expected Value
The below shows the complete derivation.
µ = ∑_(all x)▒〖x f(x; λ)〗
= ∑_(x=0)^∞▒x (e- λ λx)/x!
= e-λ ∑_(x=1)^∞ λx/(x-1)!
= λe-λ ∑_(x=1)^∞ λx-1/(x-1)!
= λe-λ eλ
= λ
µ = λ
Variance = σ2
= σ2 = ∑_(all x)▒x2f(x; λ) - µ2
= σ2 = E(x2) - (E(x))2
∑_(x=0)^∞▒x2(e-λ λx)/x!
= e-λ ∑_(x=0)^∞▒(x(x-1) + x) λx / x!
= e-λ ∑_(x=0)^∞▒(x(x-1) ) λx / x! + e-λ ∑_(x=0)^∞▒( x) λxe-λ / x!
Where e-λ ∑_(x=0)^∞▒( x) λxe-λ / x! = λ
= e-λλ2 ∑_(x=2)^∞▒( λx-2) / (x-2)! + λ
= e-λλ2eλ + λ
= λ2 + λ
E(x2) = λ2 + λ
= σ2 = λ2 + λ - λ2
= σ2 = λ
Link for playlists:
In this class, We discuss Mean and Variance of Poisson Distribution.
The reader should have a prior knowledge og poisson distribution. Click Here.
Mean = µ = Expected Value
The below shows the complete derivation.
µ = ∑_(all x)▒〖x f(x; λ)〗
= ∑_(x=0)^∞▒x (e- λ λx)/x!
= e-λ ∑_(x=1)^∞ λx/(x-1)!
= λe-λ ∑_(x=1)^∞ λx-1/(x-1)!
= λe-λ eλ
= λ
µ = λ
Variance = σ2
= σ2 = ∑_(all x)▒x2f(x; λ) - µ2
= σ2 = E(x2) - (E(x))2
∑_(x=0)^∞▒x2(e-λ λx)/x!
= e-λ ∑_(x=0)^∞▒(x(x-1) + x) λx / x!
= e-λ ∑_(x=0)^∞▒(x(x-1) ) λx / x! + e-λ ∑_(x=0)^∞▒( x) λxe-λ / x!
Where e-λ ∑_(x=0)^∞▒( x) λxe-λ / x! = λ
= e-λλ2 ∑_(x=2)^∞▒( λx-2) / (x-2)! + λ
= e-λλ2eλ + λ
= λ2 + λ
E(x2) = λ2 + λ
= σ2 = λ2 + λ - λ2
= σ2 = λ
Link for playlists:
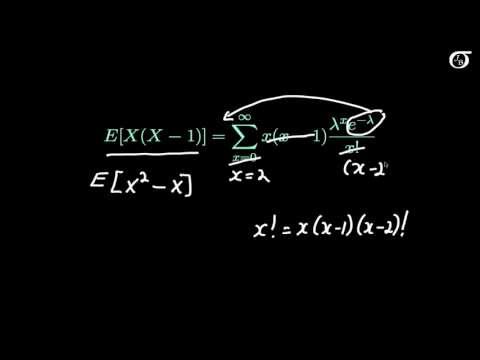 0:09:17
0:09:17
 0:05:59
0:05:59
 0:05:54
0:05:54
 0:14:30
0:14:30
 0:08:49
0:08:49
 0:10:59
0:10:59
 0:14:17
0:14:17
 0:06:54
0:06:54
 0:05:55
0:05:55
 0:09:03
0:09:03
 0:16:12
0:16:12
 0:08:36
0:08:36
 0:18:14
0:18:14
 0:02:01
0:02:01
 0:06:36
0:06:36
 0:16:21
0:16:21
 0:03:55
0:03:55
 0:24:54
0:24:54
 0:12:36
0:12:36
 0:07:23
0:07:23
 0:13:01
0:13:01
 0:27:55
0:27:55
 0:15:23
0:15:23
 0:03:06
0:03:06