filmov
tv
Finding Closed Quasigeodesics on Convex Polyhedra (talk from SoCG 2020)

Показать описание
Abstract: A closed quasigeodesic is a closed loop on the surface of a polyhedron with at most 180° of surface on both sides at all points; such loops can be locally unfolded straight. In 1949, Pogorelov proved that every convex polyhedron has at least three (non-self-intersecting) closed quasigeodesics, but the proof relies on a nonconstructive topological argument. We present the first finite algorithm to find a closed quasigeodesic on a given convex polyhedron, which is the first positive progress on a 1990 open problem by O'Rourke and Wyman. The algorithm's running time is pseudopolynomial, namely O((n^2 / ε^2) (L / ℓ) b) time, where ε is the minimum curvature of a vertex, L is the length of the longest edge, ℓ is the smallest distance within a face between a vertex and a nonincident edge (minimum feature size of any face), and b is the maximum number of bits of an integer in a constant-size radical expression of a real number representing the polyhedron. We take special care in the model of computation and needed precision, showing that we can achieve the stated running time on a pointer machine supporting constant-time w-bit arithmetic operations where w = Ω(lg b).
Finding Closed Quasigeodesics on Convex Polyhedra (talk from SoCG 2020)
SoCG YRF 2021: Enumerating All Convex Polyhedra Glued from Squares in Polynomial Time
Coarse hyperbolicity and closed orbits for quasigeodesic flows - Steven Frankel
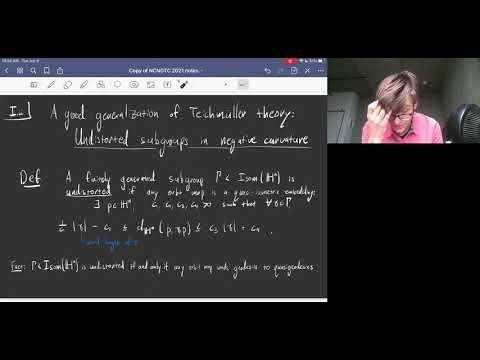
NCNGT 2021 - A quantified local-to-global principle for Anosov subgroups Part 1
Morse quasiflats Part 1 (NCNGT 2020)
Stella4D tips
Class 15: General & Edge Unfolding
Fast algorithms for geometric consensuses (SoCG 2020)
Barbara Schapira: Counting closed geodesics on hyperbolic surfaces II
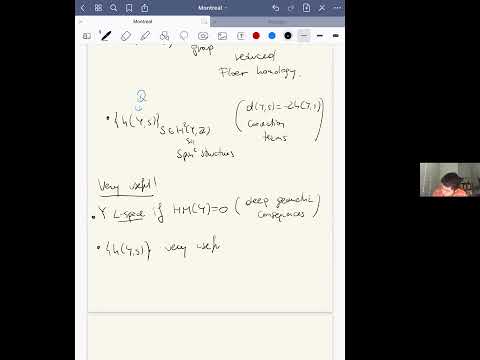
Francesco Lin : Closed geodesics and Frøyshov invariants of hyperbolic three-manifolds
Barbara Schapira: Counting closed geodesics on hyperbolic surfaces I
Convex Mirror Installation in Uttara, Dhaka (Call: 01789-636363)
Counting simple closed multi-geodesics on hyperbolic surfaces, Part 1/2 (Francisco Arana-Herrera)
F. Gueritaud Lecture 1-1
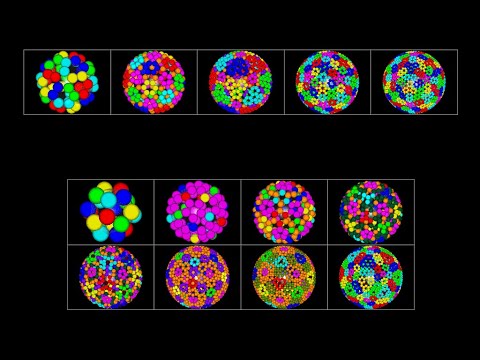
equal tangent spheres on the vertices of Goldberg polyhedron(I n, n)&(I 0, n) 2v~16v
On geometry of hyperbolic trees of spaces and Cannon-Thurston maps
Counting closed geodesics on flat surfaces (Geometry, Groups and Dynamics/GEAR Seminar)
geodesic-ellipsoid-fine-mesh
I. E. Block Lecture: Erik Demaine
Carolyn Abbott: Hyperbolically embedded subgroups of acylindrically hyperbolic groups III.
Stability in mapping class groups and right-angled Artin groups (GGD/GEAR Seminar)
Nigel Hitchin | Teichmueller spaces and the geometry of geodesics
'Regularity of Morse geodesics and growth of stable subgroups', NYGT, Sept 17, 2020, Abdul...
Webinar - Minimal Spheres in Ellipsoids - Paolo Piccione
Комментарии
 0:01:14
0:01:14
 0:58:13
0:58:13
 0:21:36
0:21:36
 0:25:08
0:25:08
 0:05:09
0:05:09
 0:50:53
0:50:53
 0:19:27
0:19:27
 1:16:09
1:16:09
 0:52:36
0:52:36
 1:10:23
1:10:23
 0:00:24
0:00:24
 0:25:55
0:25:55
 0:52:10
0:52:10
 0:02:36
0:02:36
 1:09:07
1:09:07
 0:51:53
0:51:53
 0:00:32
0:00:32
 1:10:44
1:10:44
 0:51:20
0:51:20
 0:52:37
0:52:37
 1:25:31
1:25:31
 1:06:51
1:06:51
 1:03:41
1:03:41