filmov
tv
Spain | A Nice Algebra Problem | Math Olympiad
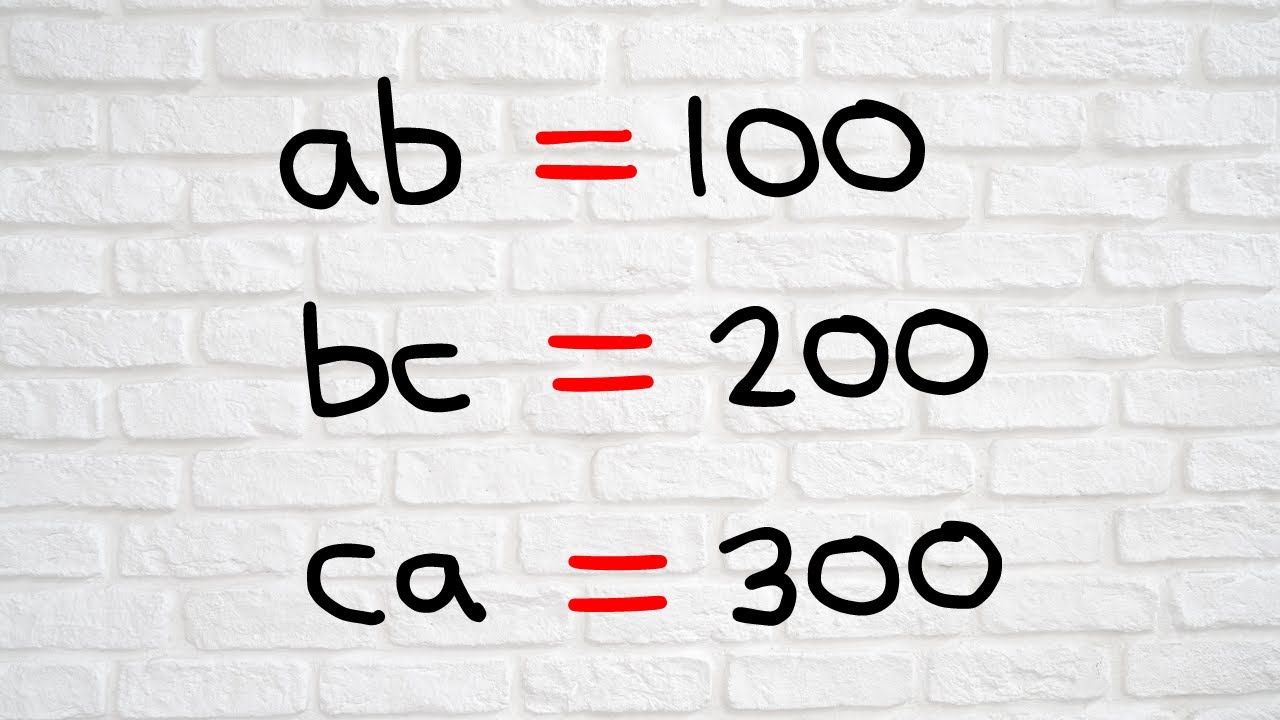
Показать описание
Hello My Dear YouTube Family 😍😍😍
Hope you all are doing well 🥰🥰🥰
If you are enjoying my video about how to solve this math olympiad algebra problem then please Like and Subscribe my channel as it helps me a lot 🙂🙂🙂
Hope you all are doing well 🥰🥰🥰
If you are enjoying my video about how to solve this math olympiad algebra problem then please Like and Subscribe my channel as it helps me a lot 🙂🙂🙂
A Very Nice Algebra Problem | Spain Math Olympiad | Find X
Spain | A Nice Algebra Problem
Spain | A Nice Algebra Problem | Math Olympiad
Spain | A Nice Algebra Problem
Spain | A Nice Algebra Problem | Math Olympiad
Spain | A Nice Algebra Problem | Math Olympiad
Spain | A Nice Algebra Problem | Math Olympiad
Spain | A very Nice Square Root Algebra Problem | Olympiad Math |
A Very Nice Algebra Problem | Spain Math Olympiad
Spain | A Nice Algebra Problem | Math Olympiad
Math Olympiad || A Very Nice Algebra Problem 🖋️✍️💯
Spain | A Nice Algebra Problem
Spain l Very Nice Olympiad Math Problem l find possible values of x=?
Spain | A Nice Algebra Math Simplification
Spain | A Nice Algebra Problem
Spain | A Nice Olympiad Math Algebra Problem
Spain | A Nice Algebra Problem | Math Olympiad
Spain | A Nice Algebra Problem
Spain | A Very Nice Square Root Algebra Problem
Spain | A Nice Algebra Problem | Math Olympiad
Spain | Math Olympiad | A Nice Algebra Problem
Spain | Math Olympiad | A Nice Algebra Problem
Spain | A Nice Algebra Problem | Math Olympiad
Spain | A Nice Algebra Problem | Math Olympiad | A Nice Exponential Equation
Комментарии
 0:06:23
0:06:23
 0:06:23
0:06:23
 0:04:29
0:04:29
 0:10:46
0:10:46
 0:11:58
0:11:58
 0:08:32
0:08:32
 0:08:09
0:08:09
 0:05:07
0:05:07
 0:06:54
0:06:54
 0:09:17
0:09:17
 0:06:36
0:06:36
 0:07:37
0:07:37
 0:10:24
0:10:24
 0:02:58
0:02:58
 0:07:05
0:07:05
 0:10:42
0:10:42
 0:11:27
0:11:27
 0:12:00
0:12:00
 0:06:48
0:06:48
 0:05:24
0:05:24
 0:10:00
0:10:00
 0:09:06
0:09:06
 0:08:58
0:08:58
 0:09:26
0:09:26