Calc 1, Lec 25B: Differential Equations (Exponential Growth, Heating & Cooling, Logistic Growth)

This is an introduction to differential equations in calculus through the examples of exponential growth and decay, Newton's Law of Heating and Cooling, and the logistic growth model.

(0:00) Review exponential growth/decay differential equation from the end of Lecture 24B. The general solution of differential equations is a family of functions (infinitely many functions), though if you add in an initial condition (like an initial population), then there is a unique solution.
(0:50) Example 1: Any function of the form y = Ce^(k*t) is a solution to the differential equation dy/dt = k*y.
(4:47) Example 2: Newton's Law of Heating and Cooling. Here solutions are exponential decay functions that have been translated vertically. This is the simplest model when spatial effects are not taken into account. Solutions take the form T = R + Ce^(-k*t), where R is the ambient room temperature. The differential equation can be written dT/dt = -k*(T - R) or, equivalently, dT/dt = k*(R - T).
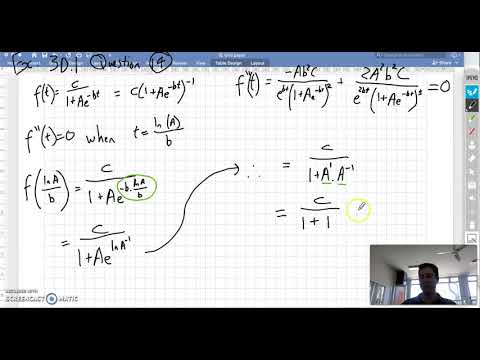
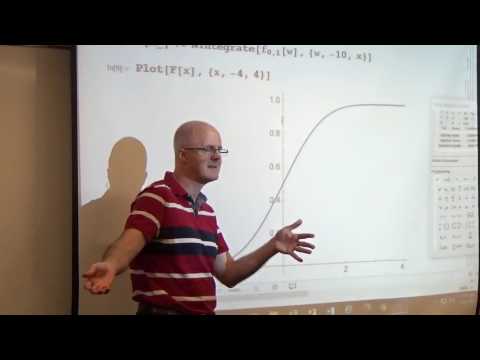
(14:41) Example 3: Logistic growth model. This is mostly used for populations that start out small and grow exponentially at first, but then level off to some "carrying capacity" L. The model takes the form dP/dt = k*P*(1 - P/L) for some positive constants k and L.
(21:29) Use DSolveValue on Mathematica to solve the differential equation. Rewrite it on the board in a different form.