filmov
tv
Intro to Solids of Revolution (3 of 3: Other axes, volume of a sphere)

Показать описание
Calculating the Volume of a Solid of Revolution by Integration
Intro to Solids of Revolution (1 of 3: Establishing the formula)
Introduction to Solids of Revolution
Disk & Washer Method - Calculus
Volumes of solids of revolution introduction
Solids of Revolution
Intro to Solids of Revolution (2 of 3: Simple worked example)
Disk, Washer and Shell Methods- Volume of Solid of Revolution
Intro to Solids of Revolution (3 of 3: Other axes, volume of a sphere)
Solids of Revolution (1 of 3: What happens when you rotate an area around an axis?)
Volumes of Revolution (Disk Method)
Solids of Revolution Intro
Introduction to Solids of Revolution
Volume of the Solid of Revolution, the Disc Method!
Volumes of Solids of Revolution: An Introduction
Calculus 1 Lecture 5.2: Volume of Solids By Disks and Washers Method
Introduction to Solids of Revolution (Disk Method around the x-axis)
Solids of Revolution P1
Disc and washer method for volume of revolution (rotated about different axis and lines)
Calculus 2: Intro to Volumes of Solids of Revolution (Disc Method)
Solids of Revolution. Circular Disk Method. Introduction
Solids of Revolution
Models for Solids of Revolution (Emma Crosswell)
Shell Method - Volume of Revolution
Комментарии
 0:11:20
0:11:20
 0:08:32
0:08:32
 0:10:40
0:10:40
 0:20:00
0:20:00
 0:08:17
0:08:17
 0:03:28
0:03:28
 0:07:34
0:07:34
 0:27:53
0:27:53
 0:09:52
0:09:52
 0:10:32
0:10:32
 0:06:23
0:06:23
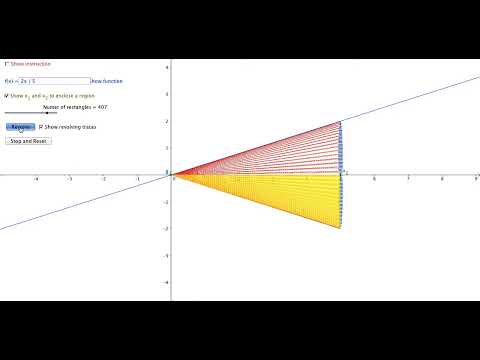 0:03:01
0:03:01
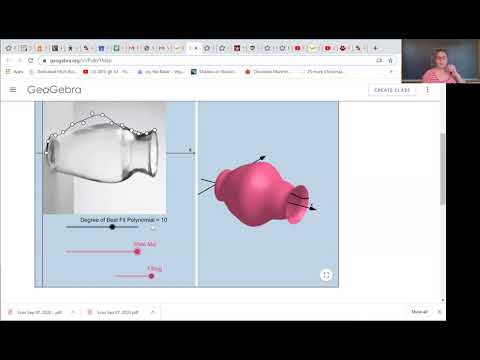 0:12:25
0:12:25
 0:08:10
0:08:10
 0:27:51
0:27:51
 2:47:49
2:47:49
 0:16:14
0:16:14
 0:12:34
0:12:34
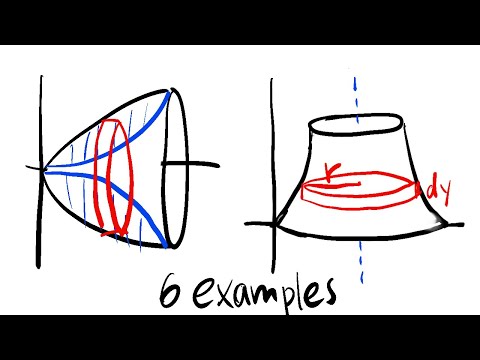 0:28:08
0:28:08
 0:09:34
0:09:34
 0:10:08
0:10:08
 0:15:43
0:15:43
 0:02:06
0:02:06
 0:12:20
0:12:20