Lecture 17: Uniform Continuity and the Definition of the Derivative

Показать описание

MIT 18.100A Real Analysis, Fall 2020
Instructor: Dr. Casey Rodriguez

We wrap up our current study of continuous functions by considering uniform continuity. We show that uniform continuity is equivalent to continuity on a closed and bounded interval, and begin to consider the derivative of a function.

License: Creative Commons BY-NC-SA

Рекомендации по теме

Комментарии

Can't believe he mentioned Borat, I love those little tidbits during these lectures.

nathanielthomas

Love the proof of the power rule! It was always so mysterious back in calculus, I thought it was actually empirical when I first learned about it. Great to see it in concrete terms!

nathanielthomas

Finally, the almighty derivative, I've been waiting for this!

nathanielthomas

Hey self-learners! Prof. Rodriguez made a conclusion at 27:40 that may cause confusion. He said "something <= epsilon" when he was trying to prove "something < epsilon". That is totally correct, given that proposition "something = epsilon" is cleary false. Given both proposition, he can conclude that "something < epsilon" is true.

That form of logical procedure is called disjunctive syllogism. One of its forms is the following.
Let A and B propositions. The rule says ( (A or B) and ¬B ) ---> A is correct.

Example:
Let A = "10 is less than 100", B = "10 is equal to 100". By disjunctive syllogism, if I have statements "10 is less or equal to 100" AND "10 is NOT equal to 100" then I can conclude "10 is less than 100".

nicolasg.b.

Very helpful lesson. Thank you Professor..🙏🙏

VaibhavSharma-zjgk

at 27:40 I believe there's a typo: you should have a "<" rather than leq for |1+1| *delta

hakus

Why at around 1:09 we can change the start and the end of the summation?

Daniel-kkkr

Lecture 17: Uniform Continuity and the Definition of the Derivative

Lecture 17: Uniform Continuity and the Definition of the Derivative

Real Analysis | Lecture 18 - Continuity And Uniform Continuity

Real Analysis | Intro to uniform continuity.

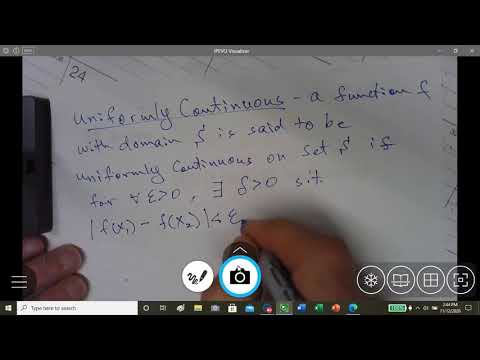
What is Uniform Continuity?

Advanced Calculus I, Part 16, Uniform Continuity and Examples, The Heine Cantor Theorem

Lecture 13.7 - Extending Uniformly Continuous Functions

Lecture 17: Continuity

Real Analysis | The uniform continuity of sqrt(x).

Sequential Characterization of Uniform Continuity

402.4Y3 What Is Uniform Continuity?

LIPSCHITZ FUNCTIONS OF ORDER ALPHA ARE UNIFORMLY CONTINUOUS

Uniform Continuity : L17 | UGC/CSIR NET, GATE, IIT JAM/ UPSC/ NBHM |

Real Analysis complete course ||Lec-17|| Uniform continuity ||Lipschitz condition

Lecture 13.4 - Uniform Continuity on Closed Intervals

Topics In Analysis (Lecture 17): Interchanging Limits

Lecture 13.8 - Derivatives of Uniformly Continuous Functions

MATH 155 X. Meeting 17 (20220428) Continuity on a Compact Set and Uniform Continuity Part 1

Lecture 17. Absolutely continuous and singular measures

How to Prove a Function is Uniformly Continuous

[78] Uniform Continuity & Riemann Integrability (Baby Rudin Chapter 2 Set Theory #4) #4.3.2.2c...

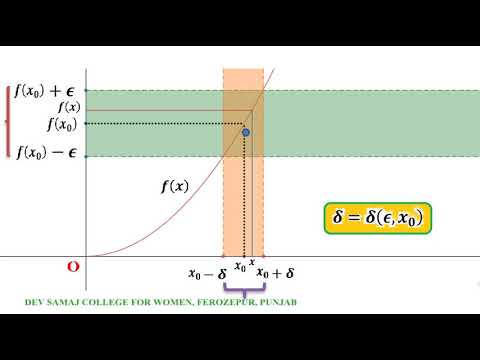
CONTINUITY AND UNIFORM CONTINUITY OF A FUNCTION OF ONE VARIABLE - A GEOMETRICAL APPROACH

MATH 155 V. Meeting 17 (20220428) Continuity on a Compact Set and Uniform Continuity Part I

3.5 Video #1 Uniform Continuity

Lecture 17.3 - Uniform Convergence and Continuity