filmov
tv
Integral Practice #4: integral of (x^3)(sqrt(x^2 + 1)) (MIT integration bee 2016 qualifying round)
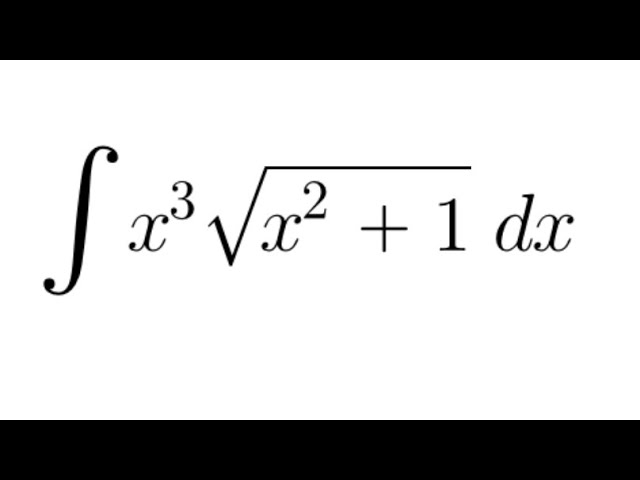
Показать описание
Hi guys! Here is my integral practice #4. Give it a try first and check the solution in the end. For integral problem requests, just comment down below. Thank you for watching! #integral #calculus
Please also check and watch the playlists of all my video tutorials:
Please also check and watch the playlists of all my video tutorials:
Integral Practice #4: integral of (x^3)(sqrt(x^2 + 1)) (MIT integration bee 2016 qualifying round)
Integration Practice (4 of 7: Exponential function area)
Integration (Calculus)
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Indefinite Integral
Basic Integration Problems
how to solve these HARD integrals
Real Analysis Question Practice For IIT JAM Mathematics 2025 | Top 250 Question Solve
Integration of Rational Functions into Logarithms By Substitution & Long Division
One weird integral trick
Calculus - Definite Integrals
Calculus 3: Line Integrals (18 of 44) What is a Line Integral? [(y)dx+(z)dy+(x)dz] Example 6
Integration By Tables
Definite Integral
Double Integrals
Lots of Basic Antiderivative / Integration / Integral Examples
Triple Integrals Practice Problems
Integration By Parts - Tabular Method
Differentiation and integration important formulas||integration formula
Basic Integration Using Power Formula
Line Integrals Practice Problems
Definite Integration Basics...How to Integrate ???
Calculus 2 - Basic Integration
Комментарии
 0:06:53
0:06:53
 0:05:46
0:05:46
 0:07:04
0:07:04
 0:22:40
0:22:40
 0:00:09
0:00:09
 0:10:47
0:10:47
 0:14:13
0:14:13
 0:09:45
0:09:45
 1:43:16
1:43:16
 0:19:20
0:19:20
 0:01:00
0:01:00
 0:07:15
0:07:15
 0:05:03
0:05:03
 0:12:40
0:12:40
 0:11:05
0:11:05
 0:25:02
0:25:02
 0:33:10
0:33:10
 0:20:34
0:20:34
 0:18:10
0:18:10
 0:00:16
0:00:16
 0:20:41
0:20:41
 0:13:00
0:13:00
 0:04:30
0:04:30
 0:26:12
0:26:12