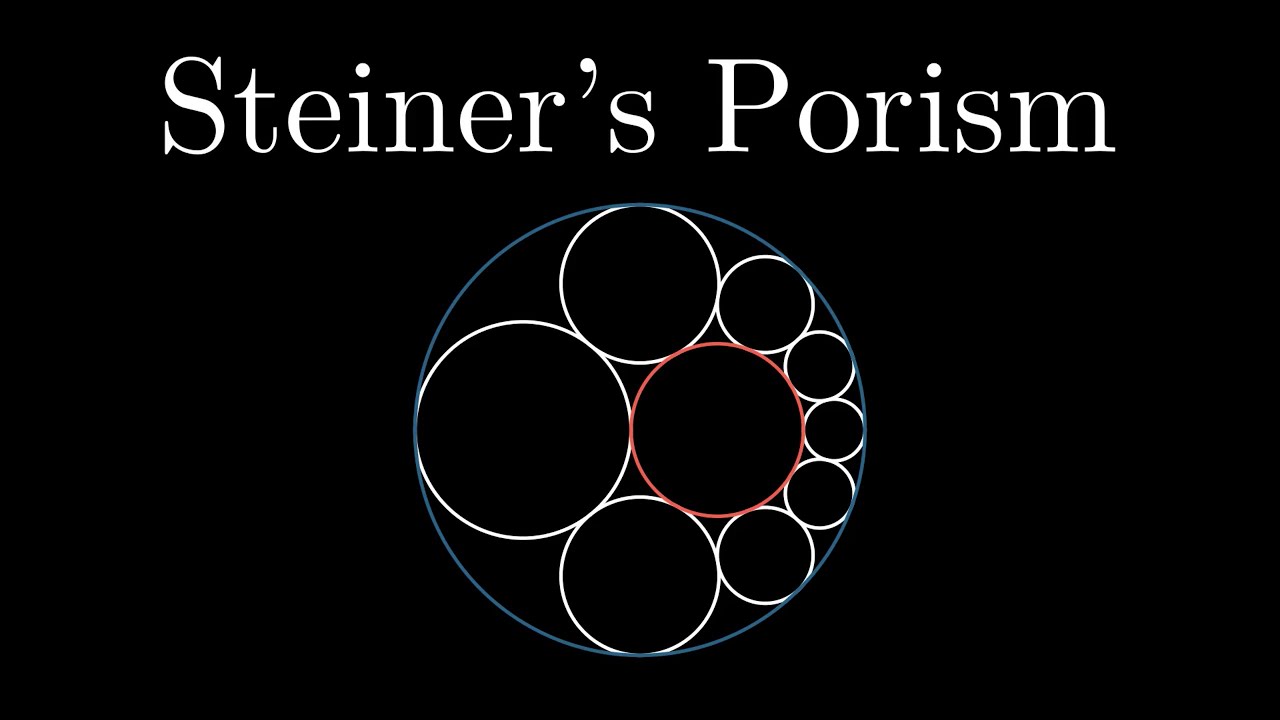
Steiner's Porism: proving a cool animation #SoME1

Strange circle stuff.
(Some people have commented that the audio is really low. Unfortunately I haven't found a way to fix it without re-uploading the whole video, but your feedback will be taken on board for the next video! Also to everyone begging for more content, I’m currently in the middle of university study, but I’m hoping to do my next video around the end of November.)

This video is my submission for 3blue1brown's Summer of Math Exposition 2021:
For more videos created by others for SoME1, here's a playlist:

Some more detail on the stereographic projection:

Animations were made in Manim:

[JxH]

13:45 "...real world applications?" Yes, arranging wire or cables within a larger circular cross section. For example, undersea power cables that might have three phases, as well as several smaller signal cables. Can be applied hierarchically !! Cheers.

[evanev]

I really like your tone, it reflects the bizarre "yeah I just thought this was cool" part of maths. I'm sharing this!

[Alorand]

The verb "to pore over something" is more clearly preserved in modern English. I like to pore over proofs of Steiner's porism.

[mimithehotdog]

Using a sphere to transform circles is so satisfying .

[sanderbos]

This was an awesome video, thank you! Nothing's more noble to pursuit than neat GIFs!

[tmgrassi]

Oh, ok, so "porism", has nothing to do with the fact that the circles look like _pores_ ? I'm slightly disappointed. The thumbnail certainly looked like a _porous_ disk to me!

But no, it turns out it's related to the English verb "to pore" instead! Well, that's still interesting.

Anyway, great video! I liked your presentation a lot.

As soon as you said "mapping circles to circles" I thought of Möbius transformations, which I used in a _Basic Complex Analysis_ course. But I didn't know how they related to the stereographic projection! This is great!

It's also nice to see the graphical version of the tangency argument, having already proved that fact analytically.

All in all, thanks for this insightful video!

[andreben]

I love how from a simple definition of the projective complex line, we end up with such sophisticated diagrams. Homographies are so neat.

[nosy-cat]

at 8:17, the discussion is not complete. There are two more possible places the circles can go and still be tangent to all three circles (red, blue and white): one is touching the blue and white circles at their intersection and touching the red circle on the other side (from the inside). The other one is similar, going from the red and white intersection to touch the blue circle on the other side. To make the proof complete, these cases should be ruled out, too. (Not that it's hard, I just thought this should be mentioned as well.)

[josephyoung]

13:19 The neat gif we were all waiting to see

[beauanasson]

I really appreciate how succinctly this video demonstrates the effectiveness of solving hard problems by first mapping them to simpler ones (in this case mapping a chain of circles of varying radii onto a chain of circles with the same radius).

[antoninashachar]

This gave me existential dread. Thank you.

[asthmen]

This is super ineresting, thank you!! The arguments are really clear & I love the animations.

The only thing I'd add is that the function is only tangent-preserving by coincidence, because you're looking at circles. More fundamentally, what your bijective function is *really* preserving is intersections (as can be seen because this is what your proof uses). Cheers!

[garlicito]

Oh I absolutely adore your style of teaching. Image my surprise learning that this was a small channel considering that this was one of the coolest math videos I’ve seen

[akerbeltz]

This is one of the best results in Projective Geometry, really nice video.

[kaiserouo]

I love that you actually drew that QED box in the end of the proof. I was somehow facinated everytime when I see that.

[DeclanMBrennan]

Beautifully explained and illustrated and that's a bizarrely simple proof leaving almost all the tools in the box and just doing some careful pondering.

[cannonball]

THANK YOU, I'VE BEEN TRYING TO FIND SOMETHING TO EVEN DEFINE THIS STRUCTURE FOR LIKE 6 MONTHS. I didn't even know the name of what this was called in Mathematics, thank you.

[isaacwalters]

You did an amazing job intuitively explaining the idea of functional continuity by the tangency preserving principle you mentioned!! Absolutely stellar

[dranorter]

I ended up pausing at 1:20 and trying to prove using circle inversion. Supposing we have one working example, choose one white circle, "W1". Draw a new circle "A" which inverts the white circle to itself, the red circle to itself, and additionally the blue circle to itself. Now, select a white circle, "W2", adjacent to the first, and similarly construct "B" which inverts that white circle to itself and also the red circle to itself and the blue to itself.

If we reflect "W1" over "B", the resulting circle "W3" will be tangent to the red and blue circles (since those map to themselves), and also to "W2" since "W1" was tangent to "W2" (which is being mapped to itself). If we reflect "W2" over "A", the resulting circle will similarly be tangent to the red circle, the blue circle, and "W1".

We can continue reflecting any new white circles over "A" or "B" (whichever one didn't generate them in the first place) to create "W4", "W5" and so on. The numbering doesn't state their spatial ordering, but as you can see, they'll form a chain since each new one will be linked to an old one. Due to their tangents, each such new circle must correspond to some white circle in the original diagram.

Because the original diagram formed a loop, this process must come to an end with some finite number of white circles.

Furthermore, we can invert the circles "A" and "B" over one another repeatedly to generate "C", "D", "E" etc., which are circles fixing the red and the blue circle, and additionally fixing "W3" or "W4" etc. IE, each white circle will have a corresponding circle which maps it to itself in addition to mapping blue to itself and red to itself. Allow me to name the collection of "A", "B", "C" etc., calling it "R". The thing to note about "R" is that each member is a symmetry of the entire figure, mapping it to itself.

Because all the members of "R" map the whole image to itself via circle inversion, the members of "R" must all intersect at the intersection of "A" and "B", since if they didn't, it would violate the symmetry. The intersection of "A" and "B" is actually two points, one inside the red circle, and one outside the blue circle. Let's put a new circle around the second intersection point, keeping it small enough that it's entirely outside the blue circle. I'll dignify this new circle with a color - it's the green circle.

If we invert all members of "R" over the green circle, something interesting happens. Because they intersect the center of the green circle, they necessarily become straight lines instead of circles. Now invert the rest of the figure - the white circles, the blue circle and the red circle - around the green circle. We know we'll end up with white circles in a chain, still tangent to the new blue and red circles. We also know our new straight lines are tangent to our new white circles. But what's really notable is that the new straight lines will be symmetries of the new white circles, since circle inversion itself preserves symmetries expressed using circle inversion.

But if our new figure is symmetrical over a collection of lines, then actually, it's rotationally symmetrical, and all the circles are the same size.

So if we rotate the white circles in our new figure, by any amount we want, and then use circle inversion over the green circle to map them back onto the old figure, then we get a working chain, and can create the desired animation.

I like this proof because its structure is a good match for the question; the stereographic proof loses me a bit when it starts trying to show the red circle can be put anywhere. (The original stipulation was that we can choose the red circle's size, not that we can choose its distance from the edge.) However, the proof in the video gives a good sense of why any size of red circle will work, and mine doesn't.

Things I omitted: Why can we construct "A" and "B"? Why can we trust that symmetries defined by circle inversion get preserved by circle inversion?

[wenhanzhou]

Very nice! Enjoyed the video from start to end.