Changing the subject of the formula | Transposition of formulae | Algebra

Показать описание

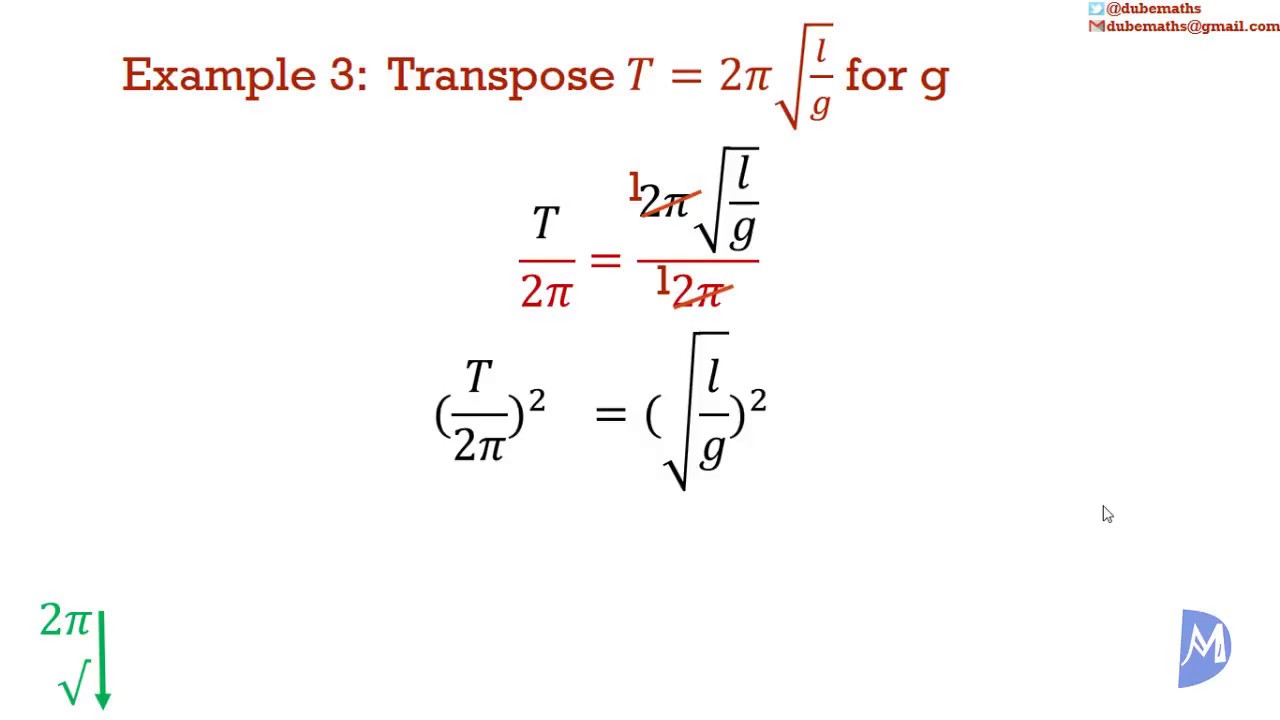
Changing the subject of the formula (also known as Transposition of formulae) is discussed. We discuss what can be done while keeping the relationships in the equation the same. We define algebraic equations and formulae. The guidelines for changing the subject of the formula are: (1) Remove all other letters/expressions from the side with the new subject - Remove in the reverse order of BODMAS; (2) If the new subject is in the denominator, isolate this fraction on one side and multiply to get it in the numerator; (3) If the new subject occurs more than once, put all the terms that contain it on the same side and factor it out; and (4) Rewrite the equation so that the new subject is on the L.H.S.
Related videos:
This topic:
Upon completion of this series of videos on this topic, you will understand/be able to:
1. use symbols to represent numbers, operations, variables and relations;
2. translate statements expressed algebraically into verbal phrases;
3. perform arithmetic operations involving directed numbers;
4. perform the four basic operations with algebraic expressions;
5. substitute numbers for algebraic symbols in simple algebraic expressions;
6. perform binary operations (other than the four basic ones);
7. apply the distributive law to factorise or expand algebraic expressions;
8. simplify algebraic fractions;
9. use the laws of indices to manipulate expressions with integral indices;
10. solve linear equations in one unknown;
11. simultaneous linear equations, in two unknowns, algebraically;
12. solve a simple linear inequality in one unknown;
13. change the subject of formulae (Including those involving roots and powers);
14. factorise algebraic expressions;
15. solve quadratic equations;
16. solve word problems (Linear equation, Linear inequalities, two simultaneous linear equations, quadratic equations);
17. solve a pair of equations in two variables when one equation is quadratic or non-linear and the other linear;
18. prove two algebraic expressions to be identical;
19. represent direct and indirect variation symbolically;
20. solve problems involving direct variation and inverse variation.

Social Media:

Remember, if you like this video, if you like what I do on this channel, please like this video.
If you are new to this channel, Please subscribe.

The vision:
Do you want to obtain excellent grades in Mathematics? Then, look no further. Upon completion, my channel will offers a complete course in Mathematics. The course is strategically structured, starting with the very basics, to cater to present and recent secondary school students, working professionals and mature candidates alike. These videos are equally great if you have never done the topic before or if you are just interested in revision.

Welcome to the experience. My aim is to help you understand Mathematics – to help you to see that Mathematics is not difficult – to show you that perseverance is the only way… Practice! Practice! Practice!

The great thing about having a course on YouTube is that you can go at your own speed – pause, replay, skip ahead at your own leisure. The most important thing is that you stick with it… a little everyday brings excellent grades your way.

In closing:
As always, my name is Mr. Dube. Join me in the next video.