filmov
tv
Why there are no 3D complex numbers
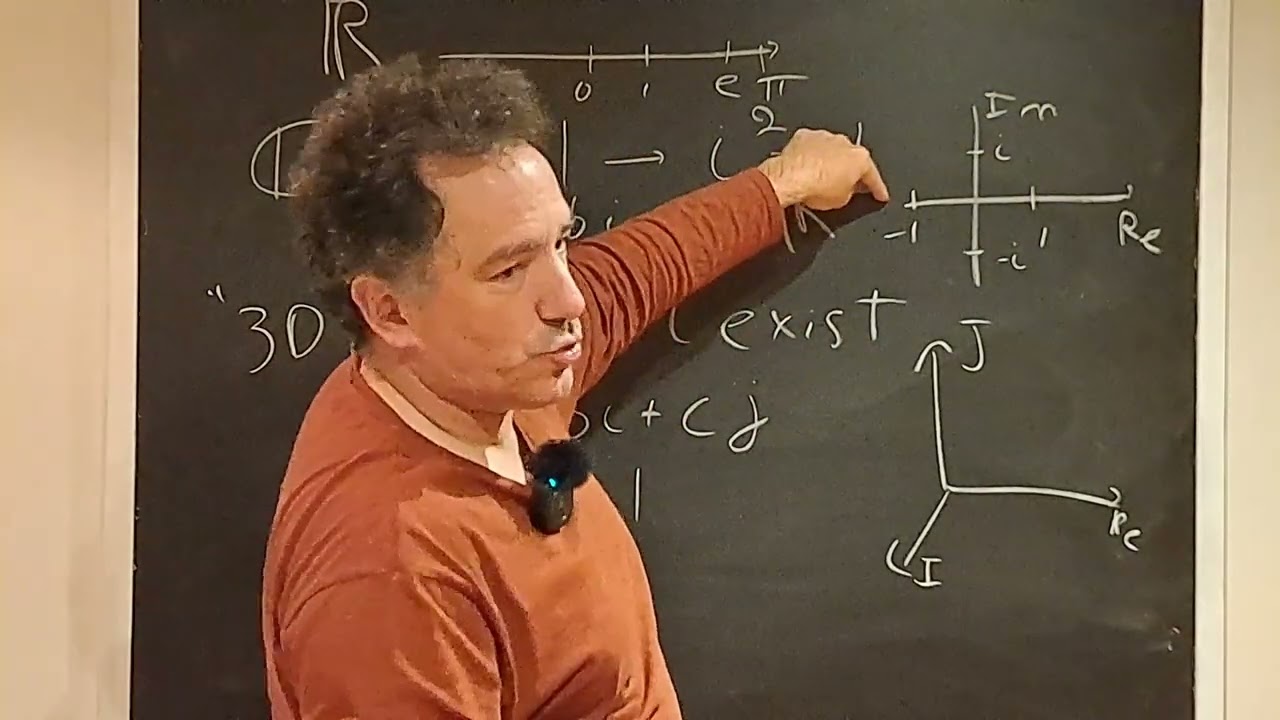
Показать описание
A simple argument as to why there are no 3D complex numbers. See the following video by Michael Penn for a more elaborate and rigorous proof.
Why are there no 3D animators on YouTube?
No 3D animators? Featuring Odd1sout, Jaiden, Illymations and Haminations. @PeterGriffin-h5d
How Would Our World Look In 4D?
these glasses help you do ONE thing
Growth of a testicular tumor #anatomy #biology #3d
Is 3D Animation Easier Than 2D Animation
as you asked me, the 3D Printed Scissor Snake is still growing 😅
3D printed illusion: Breaks the laws of physics! 🤯
I Made a 3D Spider and called it Bob. #art #drawing #3D #draw #artist #illustration
I Tested Things That Make No Sense… 😵💫🎢 #craft #3dprinting #diy
this device turns your burritos into tacos
3D printers are worse than I thought. Time to do something about it!
I Used Artlist AI to Visualize a Real Estate Project. No 3D Modeling Required
Constipation - 3d animation #meded #anatomy #3dmodel
Can you find the 5th arrow? #shorts
Strange Object Floating In Space 😧 (not what you think)
marble run maze machine - 3D printed
How to connect 3D Printed Parts!
Why Do Women Get Period Cramps ?
Is it possible to make a Hyperrealistic Cake using everyday items?
3D printed Slide Action ballpoint pen - now with rhymes! #3dprinting
3D Printed Desk Art - Coffee Floating Cup
Who says one nozzle is enough!? 3D printing with different nozzle sizes
How You'd Look Living on Different Planets - 3D Animation
Комментарии
 0:09:01
0:09:01
 0:01:49
0:01:49
 0:01:00
0:01:00
 0:00:24
0:00:24
 0:00:17
0:00:17
 0:05:55
0:05:55
 0:00:11
0:00:11
 0:00:32
0:00:32
 0:00:10
0:00:10
 0:00:45
0:00:45
 0:00:28
0:00:28
 0:19:02
0:19:02
 0:11:11
0:11:11
 0:00:21
0:00:21
 0:00:33
0:00:33
 0:00:37
0:00:37
 0:00:14
0:00:14
 0:00:41
0:00:41
 0:00:20
0:00:20
 0:00:21
0:00:21
 0:00:14
0:00:14
 0:00:44
0:00:44
 0:00:28
0:00:28
 0:09:31
0:09:31