📚 Find a vector perpendicular to a plane using the cross product

Follow us:

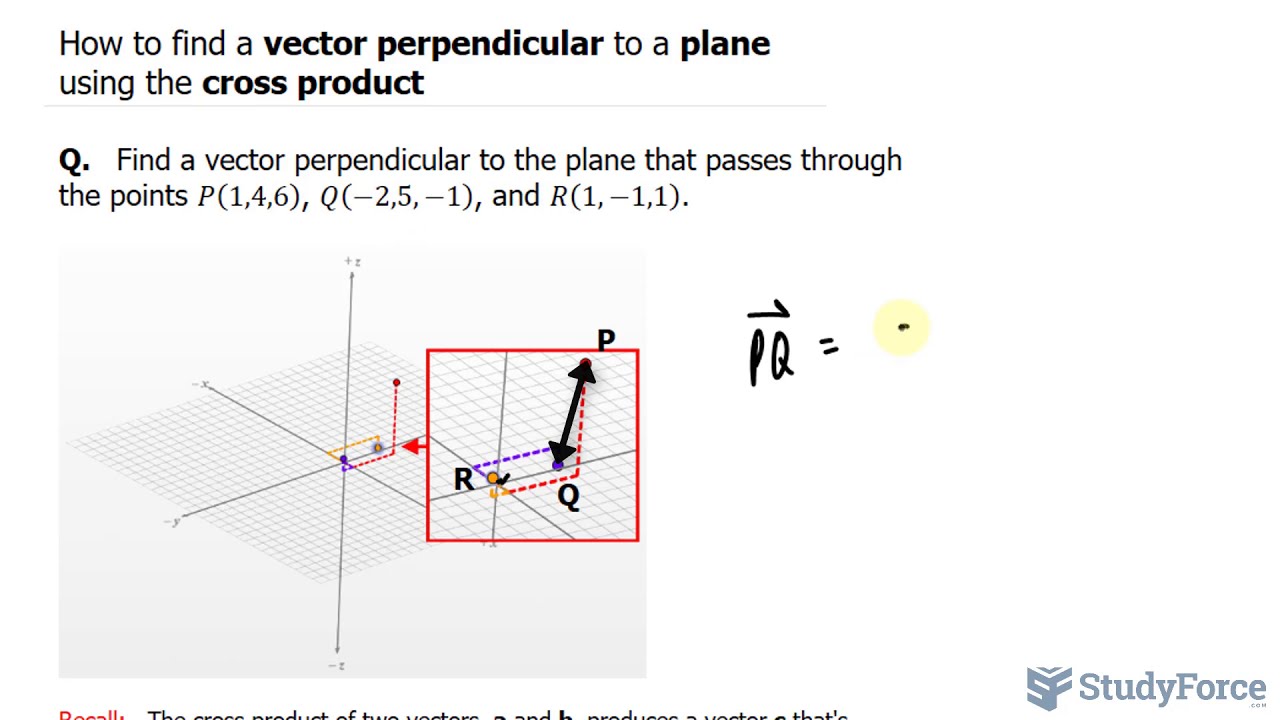
Q. Find a vector perpendicular to the plane that passes through the points P(1,4,6), Q(−2,5,−1), and R(1,−1,1).

Recall: The cross product of two vectors, a and b, produces a vector c that's perpendicular to both a and b.

Cross product: ( a×b=⟨a_2 b_3−a_3 b_2, 〖 a〗_3 b_1−a_1 b_3, 〖 a〗_1 b_2−a_2 b_1 ⟩ )

[rexclarke]

This man just saved my uni assignment xx your the best!!!

[shannonharper]

I swear you’ve worked out the vectors QP instead of PQ, and RP instead of PR

[deanrochester]

is the -40, -15, 15 the coordinates for a point that is perpendicular to the plane PQR? How can I get a point (X, Y, Z) that would makes a perpendicular vector from point R to the plane PQR?

[larrysaverinus]

Can I do instead of PQ, PR to PQ, QR??