Fractional derivatives and applications in MRI

UBC Physics & Astronomy Department Colloquium on July 8, 2021. Presented by Richard Magin (UIC).

Diffusion-weighted Magnetic Resonance Imaging (MRI) Depicts Regions of Sub- and Super-diffusion Encoded by the Fractional Diffusion Equation

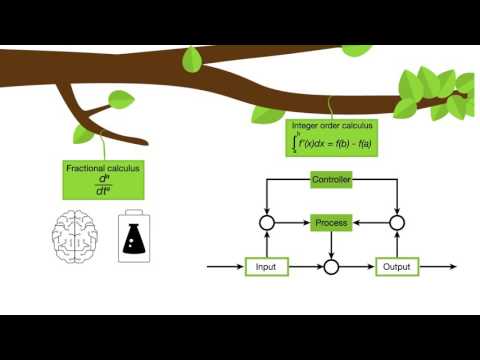
Fractional-order time and space derivatives extend the classical diffusion equation in a manner that accounts for the non-Gaussian diffusion often observed in heterogeneous materials. MRI provides diffusion-weighted images of biological tissues, which exhibit anisotropic, hindered, and restricted diffusion. Fractional calculus models of anomalous diffusion display regions of sub- and super-diffusion separated by a line of quasi-diffusion along which the mean squared displacement is a linear function of diffusion time. This behavior can be captured by fractional derivatives and/or by introducing a diffusion coefficient with a power-law decay varying as a function of time or space. The corresponding phase diagrams, like pages in a book, result in a portfolio of representations of anomalous diffusion. The anomalous phase cube employs lines of super-diffusion (Lévy process) and sub-diffusion (subordinated Brownian motion) to stitch together the different diffusion models for corresponding regions.