filmov
tv
Classical Mechanics, Lecture 7: Noether's Theorem. Two Body Problem.
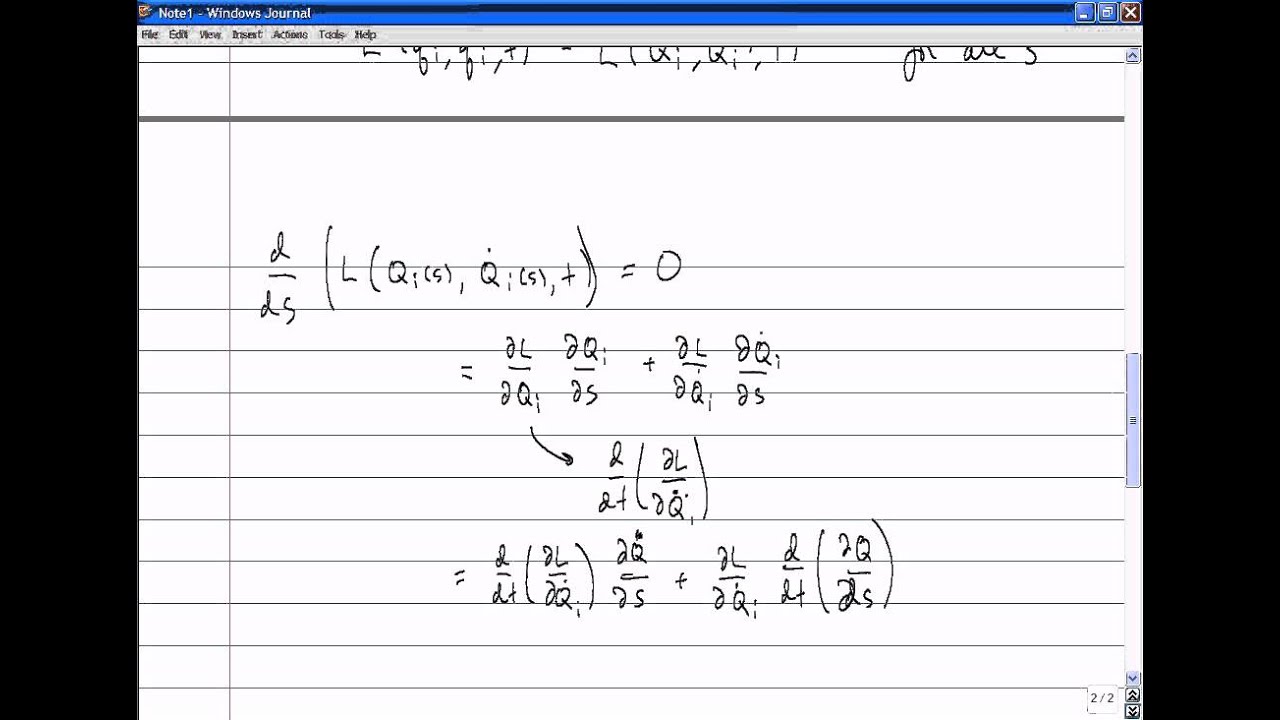
Показать описание
Lecture 7 of my Classical Mechanics course at McGill University, Winter 2010. Noether's Theorem. Two Body Problem.
The course webpage, including links to other lectures and problem sets, is available at
The written notes for this lecture are available at
The course webpage, including links to other lectures and problem sets, is available at
The written notes for this lecture are available at
Classical Mechanics, Lecture 7: Noether's Theorem. Two Body Problem.
8 - Theoretical Mechanics - Symmetries, Noether's theorem I
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
How much does a PHYSICS RESEARCHER make?
Lagrangian and Hamiltonian Mechanics in Under 20 Minutes: Physics Mini Lesson
Classical Mechanics, Lecture 17: Hamiltonian Evolution. Poisson Brackets. Noether's Theorem.
Classical Mechanics with a Bang! (2017 Fall) - Lecture #7
CLASSICAL MECHANICS. Noëther's theorem
prof. Kazimierz Rzążewski 'Quantum Mechanics' lecture 7/10
The Most Beautiful Result in Classical Mechanics
Noether's Theorem Explained (Part 1/6) - Introduction
Week 6 Video 2: Noether's Theorem and Conserved Quantities
Classical Mechanics, Lecture 4: Lagrange Multipliers. Near Equilibrium Dynamics. Oscillators.
Noether's Theorem
Symmetry and conservation laws: Noether's contribution to physics - Uhlenbeck
Energy and Momentum Conservation | Noether’s Theorem | Symmetry
Noether's theorem | Noether's theorem explained | Noether's theorem classical mechan...
Noether's theorem and Conserved Quantities (reupload)
Noether’s Theorem in Classical Dynamics : Continuous Symmetries by N. Mukunda
Classical Mechanics - Lec 05: Symmetry and Noether's Theorem
Emmy Noether: breathtaking mathematics - Georgia Benkart
Euler Lagrange Equations & Noether's Theorem | QFT
L4.10 QED: Noether's Theorem
28 - Theoretical Mechanics [solved exercises]
Комментарии
 0:48:58
0:48:58
 1:22:20
1:22:20
 0:00:38
0:00:38
 0:00:44
0:00:44
 0:18:33
0:18:33
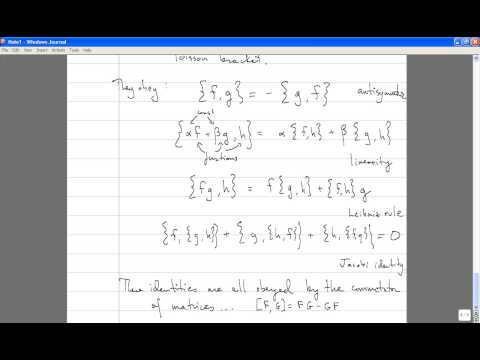 1:20:22
1:20:22
 0:47:30
0:47:30
 0:03:22
0:03:22
 1:17:15
1:17:15
 0:11:35
0:11:35
 0:19:17
0:19:17
 0:12:49
0:12:49
 1:19:30
1:19:30
 0:08:16
0:08:16
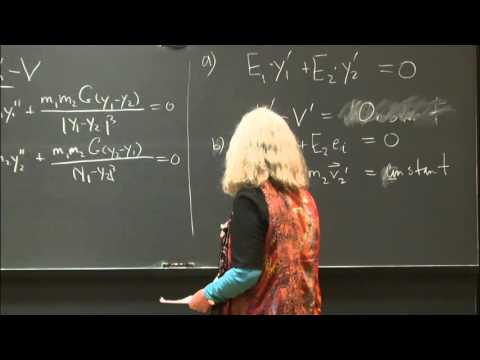 0:56:10
0:56:10
 0:06:02
0:06:02
 0:38:18
0:38:18
 0:11:09
0:11:09
 1:02:25
1:02:25
 1:26:32
1:26:32
 0:44:37
0:44:37
 0:56:22
0:56:22
 0:05:22
0:05:22
 0:35:33
0:35:33