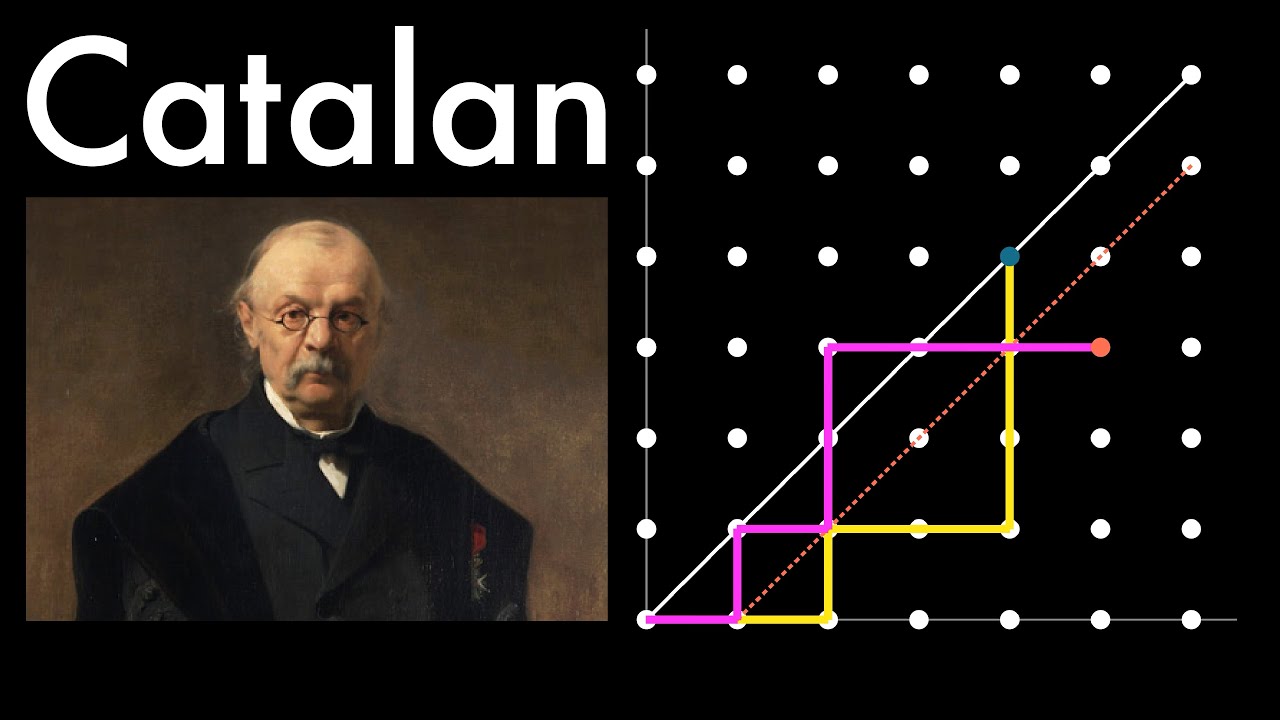
Walking city streets: Catalan Closed Form (visual proof from lattice paths)

In this video, we show how to provide a closed form for the number of northeast lattice paths to the point (n,n) that don't pass below the line y=x. The number of such lattice paths is counted by the famous Catalan numbers.

For other videos discussing lattice paths (and those mentioned in this video), check out

If you like this video, check out my others and consider subscribing. Thanks!

#catalannumbers #catalan​ #manim​ #math​ #mtbos​ ​ #animation​ #theorem​​ #visualproof​ #proof​ #iteachmath #mathematics #binomialcoefficients #latticepaths #discretemath #combinatorics #enumeration #closedform

This animation is based on the well-known interpretation of Catalan numbers as counting restricted lattice paths. I recommend the Wikipedia site or the books Enumerative Combinatorics I and II by Richard Stanley for someone wanting to know more about Catalan numbers.

To learn more about animating with manim, check out:
_________________________________________
Music in this video:

[robnicolaides]

Lovely video! Is there a proof that corresponds to an algorithm that reflects the closed form formula more directly without using the subtraction of binomial coefficients?

[UDHAV]

I had a similar question in my math test once, the question was about the number of shortest paths a man can take to reach a specific intersection of a city on the north-east line in which the roads are laid out as grid lines on a plane without counting those paths that lie below the north-east. I had a similar thinking process where I thought that to reach a specific intersection (n, n) on the northeast line with the shortest path, the man must travel n north units and n east units, therefore the total number of shortest paths are the number of possible arrangements of n north units and n east units which are equal to (2n)!/(n!n!) and since we won't include those below the north-east line, we would have to remove half the approaches and therefore (2n!)/(2(n!n!)). Not sure if it's correct doe :)

[Daniel-mtxr]

not sure which one is the previous video you refer to? thanks

[hemadhumal]

From, Where did u get this content?.. 😅