filmov
tv
Laplace Transform: Second Order Equation
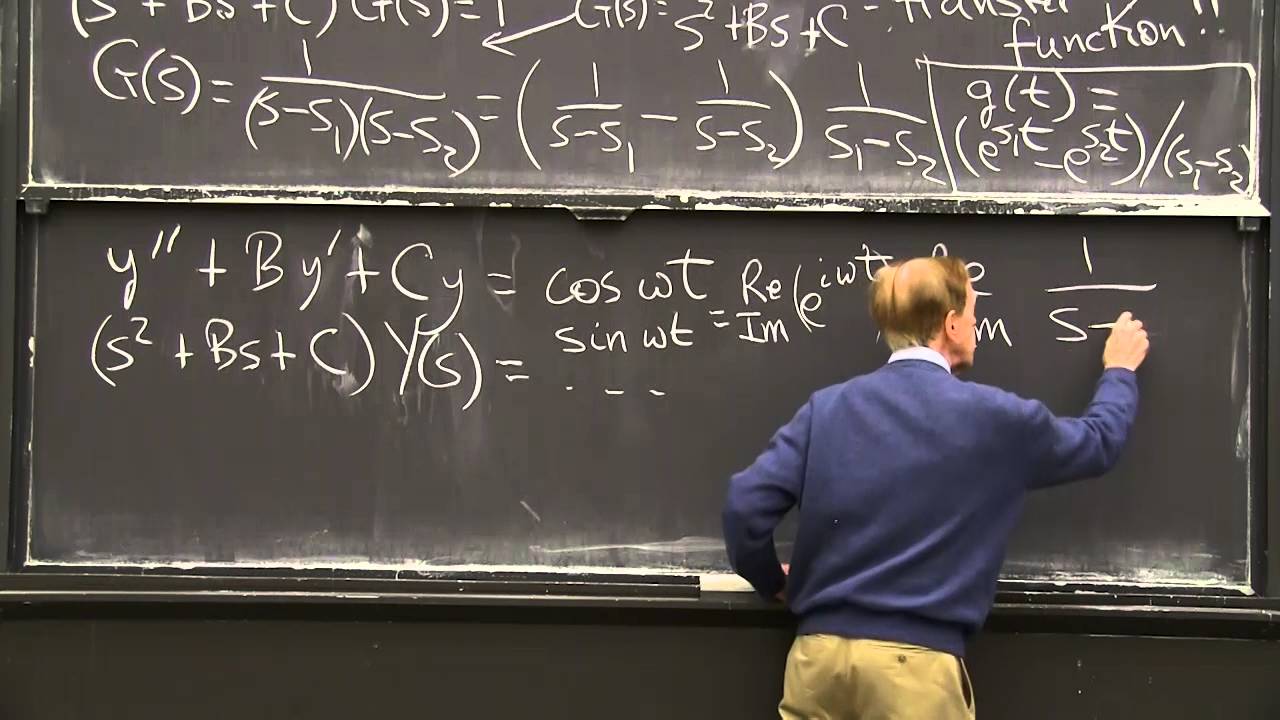
Показать описание
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler, Fall 2015
Instructor: Gilbert Strang
The algebra problem involves the transfer function. The poles of that function are all-important.
License: Creative Commons BY-NC-SA
Instructor: Gilbert Strang
The algebra problem involves the transfer function. The poles of that function are all-important.
License: Creative Commons BY-NC-SA
Laplace Transform: Second Order Equation
Laplace Transform, second order linear differential equation (part1)
How To Solve Second Order Differential Equations Using Laplace Transform
Using Laplace Transforms to solve Differential Equations ***full example***
Laplace Transform of a Piecewise Function (Unit Step Function)
How to solve differential equations
Laplace Transform | 2nd Order ODE
How To Solve Second Order Linear Non-Homogenerous Differential Equation Using Laplace Transform
Day- 4 : GIAN course on Renewable Energy Systems in Smart Grids (Course ID: 2412129)
Laplace Transform To Solve 2nd Order Differential Equation Question
Using Laplace Transform to solve Second Order Homogeneous Differential Equation.
Application of Laplace Transforms to solve a Second Order Differential Equation
solve differential with laplace transform, sect 7.5#3
Laplace Transforms of 2nd Order ODEs - Example
Second Order Equations and the Laplace Transform
Solving Second Order Differential Equations Using Laplace Transform
Solving Second order differential equation using Laplace transform example 12815
📚 How to solve second-order differential equations by the Laplace transform (Question 1)
Solution of the second-order differential equation by Laplace transform
Using Laplace Transforms to solve 2nd order non homogeneous differential equations
2nd Order Non homogeneous Differential Equation Solution using Laplace Transform - Complex Roots
Laplace Transforms and Differential Equations
What does the Laplace Transform really tell us? A visual explanation (plus applications)
Laplace Transform: First Order Equation
Комментарии
 0:16:31
0:16:31
 0:09:13
0:09:13
 0:15:14
0:15:14
 0:09:30
0:09:30
 0:06:27
0:06:27
 0:00:46
0:00:46
 0:11:38
0:11:38
 0:10:25
0:10:25
 1:48:56
1:48:56
 0:25:27
0:25:27
 0:11:56
0:11:56
 0:20:00
0:20:00
 0:07:52
0:07:52
 0:15:02
0:15:02
 0:08:20
0:08:20
 0:26:27
0:26:27
 0:12:56
0:12:56
 0:04:50
0:04:50
 0:26:12
0:26:12
 0:06:16
0:06:16
 0:30:58
0:30:58
 0:18:11
0:18:11
 0:20:25
0:20:25
 0:22:38
0:22:38