filmov
tv
Optimization of Price or Demand Function for Maximum Revenue Calculus

Показать описание
Optimization of Time Application: Find the critical numbers and analyses for optimum value
A unique series developed for the students preparing for GCSE Level A and equivalent examination globally. Anil Kumar has shared his knowledge with students who are preparing for GCSE Level A so that they can understand and perform much better.
Absolute Maximum and Absolute minimum value for any function continuous in closed interval [a, b] will always exist at the critical numbers or at the end points.
#optimization_Calculus #Increasing_Decreasing_Interval #IBSL_Calculus #IBSL_exponential_derivatives #Higher_Mathematics_Differentiation #anilkumarmath #globalmathinstitute #mcv4u
A unique series developed for the students preparing for GCSE Level A and equivalent examination globally. Anil Kumar has shared his knowledge with students who are preparing for GCSE Level A so that they can understand and perform much better.
Absolute Maximum and Absolute minimum value for any function continuous in closed interval [a, b] will always exist at the critical numbers or at the end points.
#optimization_Calculus #Increasing_Decreasing_Interval #IBSL_Calculus #IBSL_exponential_derivatives #Higher_Mathematics_Differentiation #anilkumarmath #globalmathinstitute #mcv4u
Optimization of Price or Demand Function for Maximum Revenue Calculus
Pricing Analytics: Optimizing Price
FULL TUTORIAL: Price Elasticity and Optimization in Python (feat. pyGAM)
Retail Pricing Strategy: Price Optimization & Cost Changes
Pricing optimization with AI explained
Introduction to price elasticity of demand | APⓇ Microeconomics | Khan Academy
Boosting Retail Margins: Price Optimization Strategies with Machine Learning
Boosting Retail Margins Price Optimization with ML
Consumer Optimization
The New Frontier in Price Optimization with David Simchi-Levi
How to do Price Optimization for Maximizing Profit $$$ using Demand Data
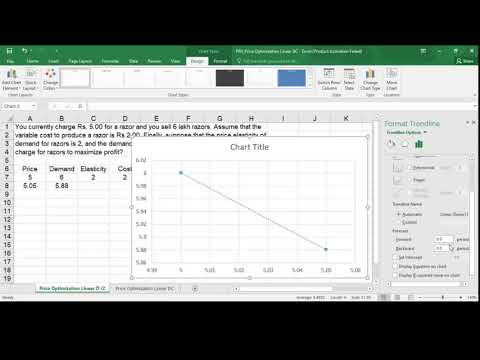
Excel solver Add-in Example || Price Optimization - 2 examples || Learn Easily
Price Optimization vs Dynamic Pricing
Price Optimization Example - Cost and Economics in Pricing Strategy
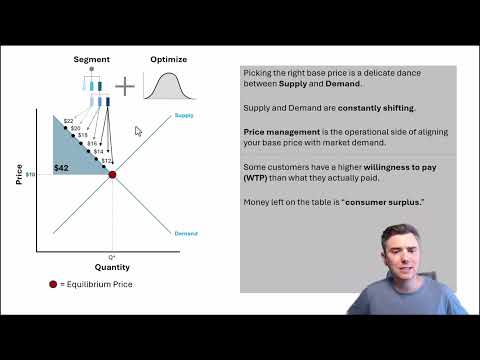
Using Supply and Demand to Explain Price Management and Price Optimization
Profit Maximization using Linear Demand Curve (Price optimization)
Economic profit for a monopoly | Microeconomics | Khan Academy
Price Optimization Excel Tutorial
lagrangians in economics: constrained optimization
Market equilibrium | Supply, demand, and market equilibrium | Microeconomics | Khan Academy
Full Tutorial: Price Elasticity and Optimization with Machine Learning in R (feat. XGBoost)
Maximizing profit through Demand-Based Pricing Optimization
Ex: Find a Demand Function and a Rebate Amount to Maximize Revenue and Profit
Optimization with Revenue, Profit, and Average Cost
Комментарии
 0:08:44
0:08:44
 0:07:54
0:07:54
 2:07:34
2:07:34
 0:05:07
0:05:07
 0:01:41
0:01:41
 0:08:40
0:08:40
 0:28:45
0:28:45
 0:36:58
0:36:58
 0:06:29
0:06:29
 0:57:42
0:57:42
 0:19:37
0:19:37
 0:08:35
0:08:35
 0:03:49
0:03:49
 0:04:01
0:04:01
 0:12:04
0:12:04
 0:09:47
0:09:47
 0:06:13
0:06:13
 1:32:52
1:32:52
 0:10:17
0:10:17
 0:10:17
0:10:17
 2:03:27
2:03:27
 0:05:06
0:05:06
 0:10:02
0:10:02
 0:20:20
0:20:20