filmov
tv
If x and y are any real numbers with x y, then there exists a rational number r ∈ Q such that x…

Показать описание
If x and y are any real numbers with x lt; y, then there exists a rational number r ∈ Q such that x lt; r lt; y. Using this density argument, show that there exists an irrational number z such that x lt; z lt; y for any real number x and y. (Hint: As √2 is an irrational number, we consider the interval (x/√2, y/√2). Then apply the density argument of Q)
Watch the full video at:
Never get lost on homework again. Numerade is a STEM learning website and app with the world’s largest STEM video library.
Join today and access millions of expert-created videos, each one skillfully crafted to teach you how to solve tough problems step-by-step.
Join Numerade today at:
#MasteringIntegrationTechniquesforOptimalResults
Watch the full video at:
Never get lost on homework again. Numerade is a STEM learning website and app with the world’s largest STEM video library.
Join today and access millions of expert-created videos, each one skillfully crafted to teach you how to solve tough problems step-by-step.
Join Numerade today at:
#MasteringIntegrationTechniquesforOptimalResults
 0:03:47
0:03:47
 0:04:55
0:04:55
 0:01:50
0:01:50
 0:01:35
0:01:35
 0:03:53
0:03:53
 0:01:28
0:01:28
 0:01:38
0:01:38
 0:00:45
0:00:45
 0:01:56
0:01:56
 0:11:53
0:11:53
 0:05:17
0:05:17
 0:01:51
0:01:51
 0:04:45
0:04:45
 0:02:12
0:02:12
 0:06:00
0:06:00
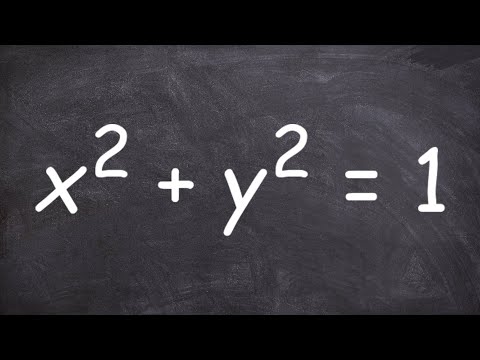 0:02:53
0:02:53
 0:02:27
0:02:27
 0:04:41
0:04:41
 0:05:26
0:05:26
 0:05:48
0:05:48
 0:03:01
0:03:01
 0:02:39
0:02:39
 0:03:33
0:03:33
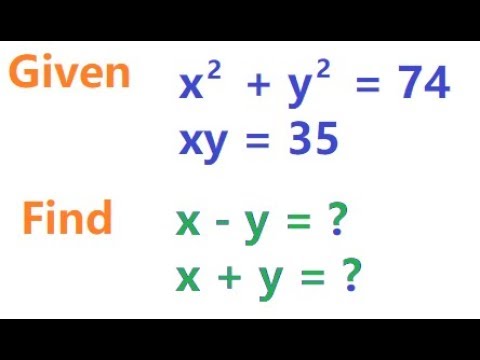 0:08:08
0:08:08